Flow Calculation from Pressure Differential Devices

Symbols
Expansion Factor
Discharge Coefficient and Flow Coefficient
Flow Equation

When installation requirements and flow conditions from ISO 5167 are met, standardized flow devices can provide flow rate results with good accuracy.

The diameter ratio is defined

β = d/D     (1)

The Reynolds number, expressing the ratio between the inertia and viscous forces in the upstream pipe is

Re_D = m/0.25 π μ₁ D     (2)

Symbols

▲ Top of Page | Symbols

Expansion Factor

The expansion factor takes into account the compressibility of the fluid.

Orifice plates

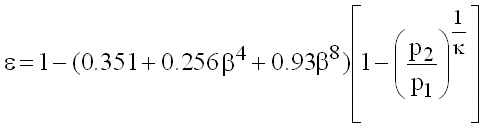(9.3)

Nozzles, Venturi nozzles, Venturi tubes

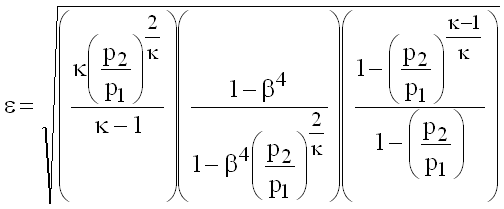(9.4)

▲ Top of Page | Symbols

Discharge Coefficient and Flow Coefficient

The discharge coefficient is defined for an incompressible fluid flow and relates actual vs. theoretical flowrate.

Orifice plates

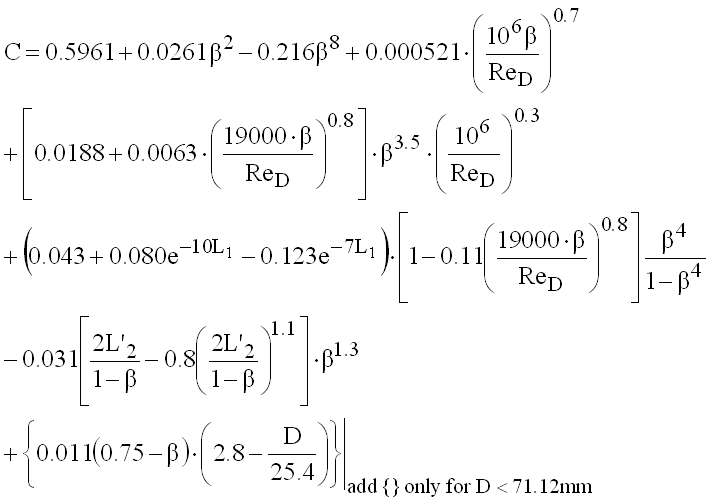(9.5)

Corner tappings: L1 = L'2 = 0
Flange tappings: L1 = L'2 = 25.4/D with D [mm]
D and D/2 tappings: L1 = 1; L'2 = 0.47

ISA 1932 Nozzles

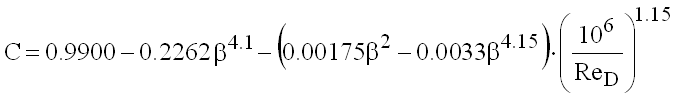(9.6)

Long radius nozzles

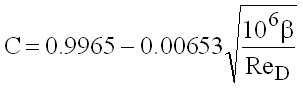(9.7)

Venturi nozzles

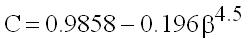(9.8)

Classical venturi tubes with an »as cast« convergent section

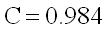(9.9)

Classical venturi tubes with a machined convergent section

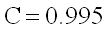(9.10)

Classical venturi tubes with a rough-welded sheet-iron convergent section

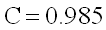(9.11)

Discharge coefficient and flow coefficient are related

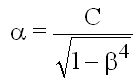(9.12)

▲ Top of Page | Symbols

Flow Equation

Where the discharge coefficient depends on the Reynolds number the mass flow can only be found by iteration.

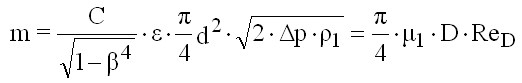(9.13)

Symbols

Content

Fluid Technology

Net Technology

Designer

Strömungsmechanik