Natural Gas Calculation - Helmholtz Energy

Symbols
Thermodynamic Properties
Functional Forms

The Helmholtz free energy is a thermodynamic potential that measures the »useful« work obtainable from a closed thermodynamic system at a constant temperature and volume. The Helmholtz energy is defined as

f ≡ u - T·s     (1)

All single-phase thermodynamic properties can be calculated as derivatives of the Helmholtz energy, as a function of temperature and density.

f(ρ,T) = f⁰(ρ,T) + f^r(ρ,T)     (2)

The dimensionless Helmholtz energy Φ uses independent variables of dimensionless density and temperature.

Φ(δ,τ) = Φ⁰(δ,τ) + Φ^r(δ,τ)     (3)

For a certain composition of a mixture the ideal Helmholtz energy is

f⁰ = h⁰ - RT - Ts⁰ = T∫T₀cp⁰dT + h₀⁰ - RT - T[T∫T₀cp⁰/TdT - Rlnρ/ρ₀ - RlnT/T₀ + s₀⁰ - Rn∑i=1x_i·lnx_i]     (4)

Φ⁰ = -ττ∫τ₀cp⁰/R·τ²dτ + h₀⁰/Rτ - 1 + τ∫τ₀cp⁰/R·τdτ + lnδ/δ₀ + lnτ₀/τ - s₀⁰/R + n∑i=1x_i·lnx_i     (5)

The ideal gas part as well as the real fluid behavior is often described using empirical models.

Symbols

▲ Top of Page | Symbols

Natural Gas Calculation - Thermodynamic Properties

The functions for calculating compressibility factor, internal energy, enthalpy, entropy, heat capacity, speed of sound and other caloric properties are all related to the Helmholtz free energy and its derivates.

Compression Factor

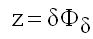(9.18)

Internal Energy

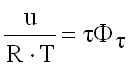(9.19)

Enthalpy

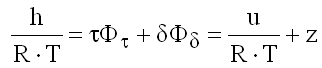(9.20)

Entropy

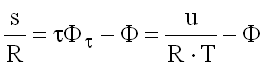(9.21)

Isochoric Heat Capacity

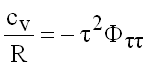(9.22)

Isobaric Heat Capacity

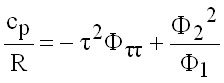(9.23)

Joule Thomson Coefficient

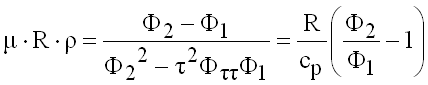(9.24)

Isentropic Exponent

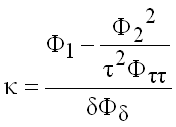(9.25)

Speed of Sound

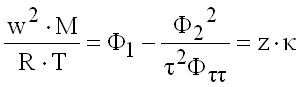(9.26)

with

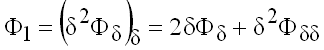(9.27)

and

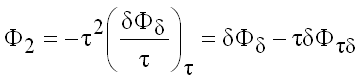(9.28)

▲ Top of Page | Symbols

Functional Forms

The common functional forms of the fundamental equations are

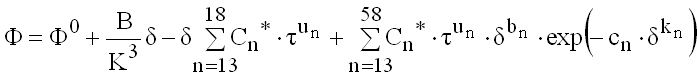(9.29)

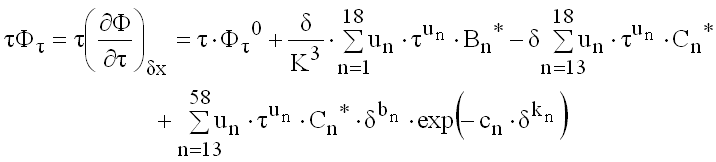(9.30)

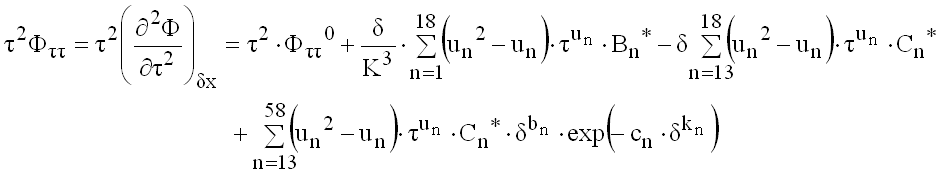(9.31)

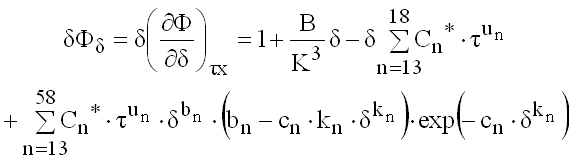(9.32)

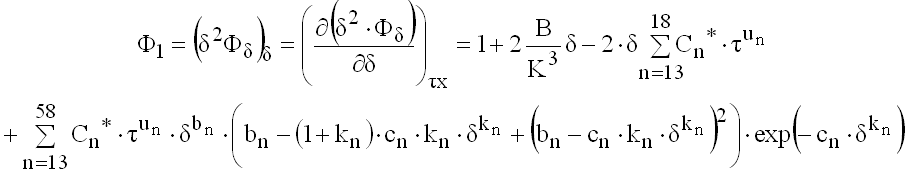(9.33)

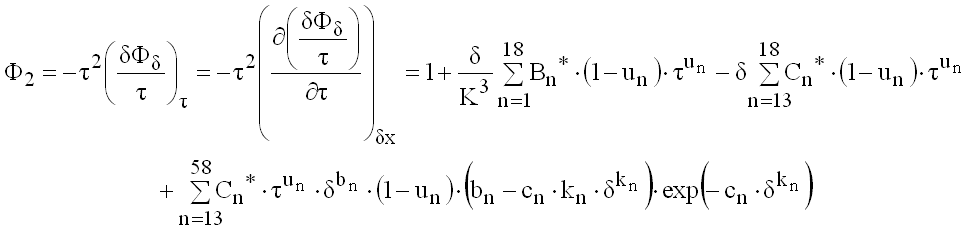(9.34)

The various constants are given in the detailed documentation for the equation of state in annex D of ISO 20765-1.

Symbols

Content