Analyse und Bewertung verschiedener Pumpgrenzkriterien für vielstufige Verdichter

Technische Universität Dresden
Fakultät für Maschinenwesen
Institut für Strömungsmechanik
Prof. Dr.-Ing. habil. Lindner

Diplomarbeit D 1479 von Axel Ebert

PDF Icon Pumpgrenze [PDF Version 1.8 MB]
ZIP Archiv Source Code [ZIP 11.6 kB]
Source Code Listing

Die Diplomarbeit wurde bei Siemens KWU durchgeführt. Sie stellt vier Kriterien vor, nach denen sich die Stabilitätsgrenze für vielstufige Axialverdichter ermitteln läßt. Als Auswertungshilfe wurde das Programm STAB geschrieben. Mit diesem läßt sich die Stabilitätsgrenze nach den einzelnen Modellen errechnen. Der Vergleich zwischen Rechnung und Messung zeigt, daß unter den gegebenen Bedingungen keines der neuen Modelle genauer ist, als das bei Siemens bislang eingesetzte Wirkungsgradkriterium. Die Arbeit ist in der leicht gekürzten Fassung, d.h. ohne Abbildung 8.2 und Abbildung 8.3, zur Veröffentlichung freigegeben.

Mülheim, 4. Juni 1992

Aufgabenstellung für die Diplomarbeit D 1479

im Studiengang Maschinenbau
in der Fachrichtung Strömungsmechanik und Thermodynamik
Name des Diplomanden Axel Ebert
Thema: Analyse und Bewertung verschiedener Pumpgrenzkriterien für vielstufige Verdichter

Zielsetzung

Beim Überschreiten der sog. Stabilitätsgrenze im Sinne abnehmenden Volumenstroms wird die Strömung in Turboverdichtern durch rotierendes Abreißen und / oder Pumpen ausgeprägt instationär, und die Schaufeln erfahren starke schwingungserregende Kräfte. Solche Betriebszustände können insbesondere bei Axialverdichtern zum Schaufelbruch führen und müssen daher vermieden werden. Hierzu ist schon während der Auslegungsphase eine möglichst genaue Kenntnis der Stabilitätsgrenze notwendig, um den zulässigen Arbeitsbereich des Verdichters vorhersagen zu können. Aus der Literatur sind verschiedene Modelle bekannt, die zur Vorhersage der Stabilitätsgrenze eingesetzt werden (u.a. /1/ , /2/ , /3/).

Diese sind hinsichtlich ihres Gültigkeitsbereiches (radial/axial, ein-/ mehrstufig) zu untersuchen und zu bewerten.

Für die rechnerische Bestimmung der Stabilitätsgrenze sollen ausgewählte Modelle in das bei Siemens/TGRM-V zur Verdichterauslegung und -nachrechnung eingesetzte Kennfeldrechenprogramm DYNATECH implementiert werden.

Die Ergebnisse der verschiedenen Modelle sind mit den bisher bei TGRM-V zugrundegelegten Stabilitätsgrenzverläufen und, soweit vorhanden, mit Meßergebnissen zu vergleichen. Ziel der Arbeit ist die Analyse der Rechenergebnisse und eine Empfehlung, welche(s) Modell(e) künftig bei TGRM-V zur Vorausbestimmung der Pumpgrenze einzusetzen ist (sind).

Betreuer
Prof. Dr.-Ing. habil. Lindner (betreuender Hochschullehrer)
Dr.-Ing. Janssen (Siemens AG KWU TGRM-V)

Fachrichtungsleiter
Prof. Dr.-Ing. habil. Vollheim

Ausgehändigt am 02.03.1992

Das stationäre Verhalten eines Verdichters ist durch seine Charakteristik gekennzeichnet, welche z.B. durch das Druckverhältnis als Funktion des Massendurchsatzes beschrieben wird. Diese Charakteristik ist zu kleinen Massenströmen hin durch die sog. Stabilitäts- oder Pumpgrenze eingeschränkt.

Bei Überschreitung einer gewissen aerodynamischen Belastung wird die Verdichterströmung plötzlich und scheinbar ohne Vorankündigung instabil. Dieses Verhalten wird verursacht durch die strömungsmechanischen Phänomene der "rotierenden Abreißströmung" und des "Pumpens", besser bekannt als "Rotating Stall" und "Surge". Betrieb im Rotating Stall führt zu einer schwingungsmechanischen Beanspruchung der Maschine. Insbesondere stellen die umlaufenden Stall-Zellen für die Schaufeln eine starke Erregung dar, deren Frequenz wegen der meist unbekannten Anzahl und Umlaufgeschwindigkeit der Zellen nicht bekannt ist. Pumpen tritt je nach Vedichterdruckverhältnis und Größe des Verbrauchervolumens mehr oder weniger stark auf. Es kann durchaus zur Zerstörung der Beschaufelung führen.

Betriebszustände, bei denen die genannten Erscheinungen auftreten, sollten daher vermieden werden. Hierzu ist schon während der Auslegungsphase eine möglichst genaue Kenntnis der Stabilitätsgrenze notwendig, um den zulässigen Arbeitsbereich des Verdichters vorhersagen zu können.

Aus der Literatur sind verschiedene Modelle bekannt, die zur Vorhersage der Stabilitätsgrenze eingesetzt werden, u. a. /1/, /2/, /3/. Die bekannten Modelle sind hinsichtlich ihres Gültigkeitsbereiches (radial/axial, ein-/mehrstufig, etc.) zu untersuchen und zu bewerten. Für die rechnerische Bestimmung der Stabilitätsgrenze sollen ausgewählte Modelle in das bei TGRM-V zur Verdichterauslegung und -nachrechnung eingesetzte Kennfeldrechenprogramm DYNATECH implementiert werden.

Die Ergebnisse der verschiedenen Modelle sind mit den bisher bei TGRM-V zugrunde gelegten Pumpgrenzverläufen und, soweit vorhanden, mit Meßergebnissen zu vergleichen. Ziel der Arbeit ist die Analyse der Rechenergebnisse und eine Empfehlung des oder der in der Zukunft bei TGRM-V einzusetzenden Modell(e) zur Vorausbestimmung der Pumpgrenzlage.

Janssen, 8.11.1990

/1/ Lieblein, S. Loss and Stall Analysis of Compressor Cascades., Trans. of the ASME, J. of Basic Eng. (1959).

/2/ Traupel, W. Thermische Turbomaschinen, Bd. II, Springer-Verlag, Berlin-Heidelberg-New York (1982).

/3/ Koch, C.C. Stalling Pressure Rise Capability of Axial Flow Compressor Stages, ASME Paper No. 81-GT-3 (1981).

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Einleitung

Die bei Siemens entworfenen vielstufigen Axialverdichter sind Komponenten von offenen Gasturbinenanlagen. Sie werden zur Stromerzeugung in Kraftwerken eingesetzt und arbeiten deshalb mit nahezu fester Drehzahl.

Für die Verdichter kann die Turbine als nachgeschaltetes Drosselorgan betrachtet werden. In Abhängigkeit vom Druck am Turbineneintritt kann der Verdichterdurchsatz unterschiedlich sein. Dabei darf der Massenstrom niemals so klein werden, daß die sogenannte Pumpgrenze überschritten wird. Diese begrenzt bei höheren Drehzahlen den stabilen Arbeitsbereich des Verdichters.

Die experimentelle Bestimmung der Pumpgrenze ist sehr kostspielig und nur bis zu Drehzahlen von ca. 85% der Nenndrehzahl sinnvoll. Darüber würde ein Anfahren der Pumpgrenze zur Zerstörung der Verdichter- und Turbinenbeschaufelung führen. In diesem Bereich läßt sich die Stabilitätsgrenze nur theoretisch ermitteln.

Genaue Stabilitätsmodelle sind also sehr wichtig. Gerechnete Pumpgrenzpunkte könnten mit gemessenen verbunden werden und so die Stabilitätsgrenze im gesamten Fahrbereich darstellen. Dieser muß überall einen sicheren Abstand zur Pumpgrenze aufweisen.

Nachfolgend werden vier Stabilitätskriterien für Axialverdichter erläutert. Sie sind in ein Auswertungsprogramm eingearbeitet, welches gleichfalls beschrieben wird. Zur Bewertung der Modelle werden die Rechenergebnisse mit vorhandenen Meßdaten verglichen.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Formelzeichen

absolute Strömungsgeschwindigkeit

Auftriebsbeiwert

Reibungskoeffizient aus Wandschubspannung und ρ/2v²

Enthalpiekoeffizient

Diffusionszahl

Deq

äquivalente Diffusionszahl

Schaufelkanalweite

Δhs

isentroper Anstieg der statischen Enthalpie

Formfaktor δ*/δ**

Inzidenzwinkel (Fehlanströmung): α1-αs1 für das Leitrad oder β1-βs1 für das Laufrad

Referenzwert des Inzidenzwinkels für minimale Strömungsverluste: ergibt sich aus dem Mittelwert zwischen den Inzidenzwinkeln i, bei denen die Verluste ω das Doppelte des Minimalwertes erreichen

Länge der kreisbogenförmigen Skelettlinie eines Profils, das dieselbe Wölbung wie das entsprechende NACA65 Profil besitzt

Massenstrom

mS*

relativer Massenstrom am Saugstutzen, auf Normbedingungen reduziert und auf den Auslegungszustand bezogen

relative Drehzahl, auf Normbedingungen reduziert und auf die Nenndrehzahl bezogen

statischer Druck

Ruhedruck

Radius

Reynoldszahl

Sehnenlänge

Teilung

Umfangsgeschwindigkeit

Strömungsgeschwindigkeit allgemein

relative Strömungsgeschwindigkeit

Δz

Axialspalt zwischen benachbarten Gittern

absoluter Strömungswinkel zur meridionalen Strömungsrichtung

αs

äquivalenter Schaufelwinkel für das Leitrad zur meridionalen Strömungsrichtung

relativer Strömungswinkel zur meridionalen Strömungsrichtung

βs

äquivalenter Schaufelwinkel für das Laufrad zur meridionalen Strömungsrichtung

Deviationswinkel (Minderumlenkung): α2-αs2 für das Leitrad oder β2-βs2 für das Laufrad

δ*

Summe der Verdrängungsdicken der Grenzschicht von Profilober- und Unterseite

δ**

Summe der Impulsverlustdicken der Grenzschichten von Profilober- und Unterseite

Wölbungswinkel: αs1-αs2 oder βs1-βs2

πR

Ruhedruckverhältnis für die gesamte Beschaufelung

Durchflußzahl als cax2/u2

Dichte

Solidity (Gitterdichte): s/t

Verlustzahl = ΔpR/(pR1-p1)

Druckzahl = Δhs/u2²

Stokesche Stromfunktion

Staffelungswinkel

Radialspiel

Indices

Auslegungspunkt

Schaufeleintrittskante

Schaufelaustrittskante

Axialkomponente

Laufrad

Leitrad

Saugseite

Umfangskomponente

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Das Dynatech - Kennfeld - Rechenprogramm

Das Programm HTO300 wurde 1970 von der Dynatech Corporation [1] entwickelt. Es dient u.a. der Nachrechnung von Strömungen durch Axialverdichter und soll an dieser Stelle kurz erläutert werden, da auf die Ergebnisse dieses Programms im Rahmen der Stabilitätsuntersuchungen zurückgegriffen wird. Alle Rechnungen betreffen Profile der NACA65 - (A10) Reihe.

Die Meridianströmungsrechnung beruht auf einem zweidimensionalen Stromlinienkrümmungsverfahren und liefert die radiale Verteilung der Strömungsgrößen entlang der Maschinenachse.

Vorgegeben wird die Gittergeometrie und der Eintrittszustand in den Verdichter. Druck und Temperatur werden in der Regel mit Normbedingungen (101,3 kPa und 15°C) festgelegt. Massenströme und Drehzahlen sind dann automatisch normiert. Eine Normierung ist für all jene Fälle wichtig, in denen Kennfelder mehrstufiger Maschinen ähnlichkeitstheoretisch richtig verglichen werden müssen.

Die Nachrechnung erfolgt nach Smith [2] unter der Berücksichtung des radialen Gleichgewichts zwischen den Schaufelreihen. Profilverluste und Randzoneneffekte werden über empirische Korrelationen erfaßt, wie es in der Praxis zur Zeit noch üblich ist.

Im Programm wird das Fluid als ideales Gas angenommen. Die Strömung gilt als:

stationär
reibungsfrei
kompressibel
rotationssymmetrisch

Es gibt keinen Massen-. Impuls- oder Energieaustausch zwischen den einzelnen Stromröhren.

Für die Umlenk- und Verlusteigenschaften der Schaufelgitter wird auf empirische Korrelationen aus umfangreichen NACA-Messungen an ebenen Gittern zurückgegriffen. Diese beruhen auf der von Lieblein/Schwenk/Broderick [5] eingeführten Diffusionszahl D für minimale Profilverluste. Conrad, der 1965 die verschiedensten Verlustkriterien verglichen hatte, weist in seiner Arbeit [4] darauf hin, daß gerade D ein brauchbares Kriterium zur Bestimmung der Impulsverlustdicke der Grenzschichten am Gitteraustritt ist. Sie wird in der Form δ**/s als Maß für die Belastung eines Gitters angesehen. D ist definiert als

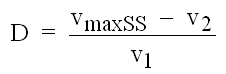Gleichung 3.1 (3.1)

In [4] wird gezeigt, wie man von Gleichung (3.1) zur nachfolgenden Gleichung (3.2) kommt. Mit Gleichung (3.2) läßt sich D aus den Gitterdaten am Ein- und Austritt berechnen:

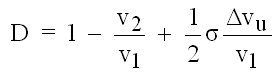Gleichung 3.2 (3.2)

Wenn für ein ebenes Gitter angenommen wird, daß vax1 = vax2, kann Gleichung (3.1) in der folgenden Form geschrieben werden:

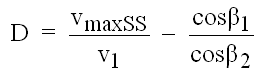Gleichung 3.3 (3.3)

Abbildung 3.1 verdeutlicht am Beispiel eines Laufrades die Winkeldefinitionen, die für die Umlenkeigenschaften der betrachteten Profile von Bedeutung sind.

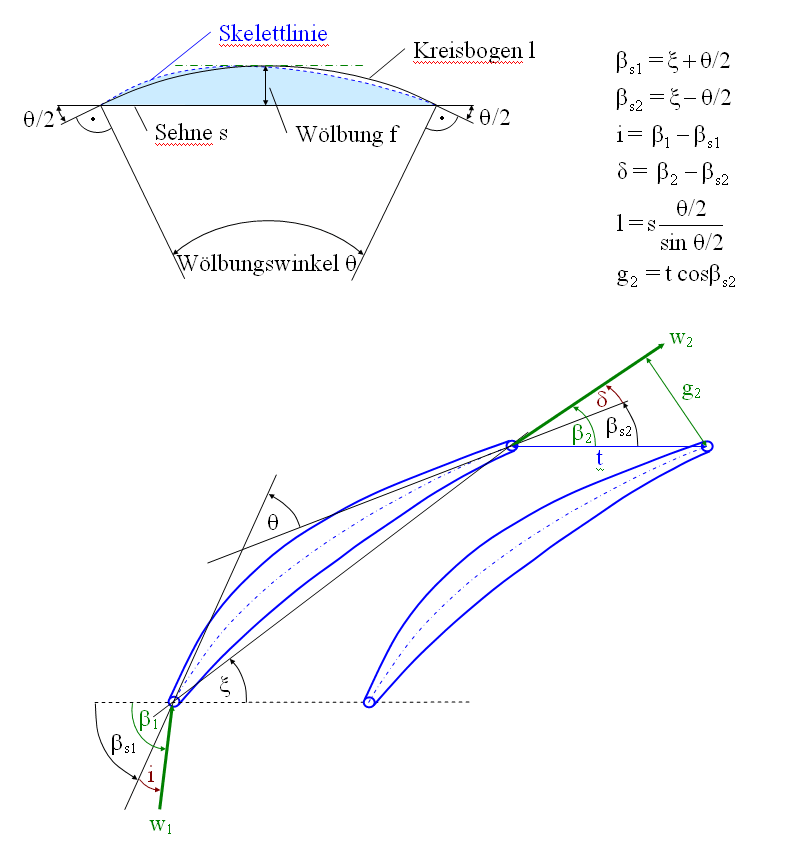
Abbildung 3.1: Winkeldefinitionen für NACA 65 Profile am Beispiel eines Laufrades

Der Inzidenzwinkel i charakterisiert die Fehlanströmung, der Deviationswinkel δ die Minderumlenkung. Das Schaufelprofil wird über den Wölbungswinkel θ und äquivalente Schaufelwinkel definiert, die sich aus einem Profil mit kreisbogenförmiger Skelettlinie ergeben, welches die gleiche Wölbung hat wie das entsprechende NACA65 Profil. Das Verfahren wird bei Johnson/Bullock et al [5] beschrieben und wird angewandt, da die Steigung der NACA65 Skelettlinie an den Vorder- und Hinterkanten gegen unendlich strebt.

Im Dynatech Programm werden die in Johnson/Bullock/Lieblein [5] zusammengetragenen Korrelationen für die Berechnung der aerodynamischen Gitterbelastung übernommen. Danach wird der Auslegungsinzidenzwinkel i* nach Liebleins Angaben in [5] berechnet und für abweichende Schaufeldicken und höhere Machzahlen (M<1) korrigiert. Hierzu wird ein korrespondierender Deviationswinkel berechnet und in Abhängigkeit von der Diffusionszahl D aus Gleichung (3.3) der tatsächliche Deviationswinkel δ gebildet. Das Verhältnis vmaxSS/v1, das zur Bestimmung von D wichtig ist, wird nach Vorschlägen von Jansen/Moffatt in [6] ermittelt. Über D und die Beziehung zur Impulsverlustdicke am Gitteraustritt wird der Verlustkoeffizient berechnet.

Die Meßergebnisse, auf die sich die Autoren in [5] berufen, stammen von Herrig/Emery/Erwin [7] und Emery/Dunavant [8]. Die erste Arbeit ermöglicht insbesondere, die bei Fehlanströmungen höheren Verluste zu berücksichtigen. Die zweite Arbeit korrigiert die Verlustbestimmung bei größeren Machzahlen.

Die Verdrängungswirkung der Wandgrenzschichten wird mit Hilfe von Blockierungsfaktoren erfaßt und nach einer Methode von Jansen [9] berechnet. Für zusätzliche Randzonenverluste im Bereich der Schaufelspitzen wird dem Programm ein zusätzlicher Verlustkoeffizient vorgegeben. Damit wird eine Verlustparabel gebildet, welche den Profilverlusten über der Schaufelhöhe überlagert wird.

Der Arbeitsbereich wird durch Zuströmbedingungen abgegrenzt, bei denen die Verlustzahl ω für ein Gitter den doppelten Wert ihres optimalen Vergleichswertes hat. Im Dynatech Programm bestimmt also ω explizit das Gebiet zwischen Stabilitäts- und Schluckgrenze.

Das Kennfeld wird gewöhnlich für einen Drehzahlbereich vom 0,7 - bis 1,05 - fachen der Nenndrehzahl und die verschiedensten Drosselzustände berechnet. Gegebenenfalls kann die Stellung der Leitschaufeln durch das Programm variiert werden.

Mangel des Programms ist, daß sich instationäre Effekte und ihr Einfluß auf die Gesamtcharakteristik eines Verdichters nicht vorhersagen lassen. Gerade bei Betrachtungen an der Stabilitätsgrenze wäre es aber erforderlich, die periodische Wirkung von Gaskräften und die zeitabhängige Anfachung und Dämpfung von Störungen verfolgen zu können.

Die in der vorliegenden Arbeit behandelten Stabilitätsuntersuchungen können natürlich nicht exakter sein als die vorgelegten Dynatech Ergebnisse. Sie bleiben deshalb auch auf halbempirische Betrachtungen beschränkt.

Der Einsatz instationärer Berechnungsverfahren könnte in vielem genauere Ergebnisse liefern, besonders wenn er mit analytischen Grenzschichtbetrachtungen gekoppelt wäre. Befriedigende Lösungen für vielstufige Verdichter existieren auf diesem Gebiet jedoch noch nicht.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Zur Instabilität von Verdichtern

Axialverdichter sind Turbomaschinen, die in der Kraftwerkstechnik, in der Schwerindustrie aber auch bei Flugzeugtriebwerken eine wichtige Rolle spielen. Sie sind so ausgelegt, daß sie den Druck einer stetigen rotationssymmetrischen Strömung erhöhen. Die Charakteristik eines Verdichters läßt sich als Funktion des Druckverhältnisses über dem Durchsatz am Saugstutzen darstellen. Als Parameter für zwei Kennlinienscharen gelten die feste Drehzahl für die Drosselkurven und konstanter Wirkungsgrad für die Muschelkurven. Die Steigung der Drosselkurven ist in ihrem jeweiligen Bereich des relativen Wirkungsgradmaximums ("gesunder Bereich") fast immer negativ. Das bedeutet, daß mit kleinerem Massendurchsatz der Druckanstieg größer wird. Diese Charakteristik ist ab einem kritischen Wert für den Massenstrom eingeschränkt, denn unterhalb dieses Wertes ist die Strömung nicht mehr stabil. Einerseits wäre es wünschenswert, eine Anlage so dicht wie möglich am kritischen Punkt zu betreiben - das brächte z. B. bei Kopplung mit einer Gasturbine eine verbesserte Nutzleistung; andererseits könnte eine geringfügige Änderung des Durchsatzes dazu führen, daß das System in den instabilen Bereich gedrückt werden würde.

Grob unterteilt lassen sich vier Zustände einer Strömung beschreiben:

rotationssymmetrisch und stationär
nicht rotationssymmetrisch und stationär
rotationssymmetrisch und instationär
nicht rotationssymmetrisch und instationär

Sie vertreten nach Mc Caughan [10] die folgenden Betriebserscheinungen:

Auslegungszustand
Rotierende Abreißen (Rotating Stall)
Tiefes Pumpen (Deep Surge)
Mildes Pumpen (Classic Surge)

Das Rotierende Abreißen ist durch eine oder mehrere Zellen mit abgerissener Strömung gekennzeichnet, die die Beschaufelung mit etwa der halben Maschinendrehzahl umlaufen. Die Ablösung kann sich entweder über nur einen Teil der Schaufelhöhe oder aber über die volle Höhe erstrecken. Für einen sich mit diesen Zellen mitdrehenden Betrachter wäre die Strömung stationär; für die Schaufeln im betreffenden Bezugssystem trifft das nicht zu. Die Leistungsübertragung ist in dem Zustand um vieles geringer als noch kurz davor. Die Schaufeln selbst werden durch den ständigen Wechsel zwischen abgerissener und anliegender Strömung sehr hoch belastet. Es kommt zu starken Vibrationen und in kürzester Zeit zu Schwingungsbrüchen.

Pumpen entsteht durch selbsterregte axiale Schwingungen der Gasmasse in Rohrnetz und Verdichter. Die Periodendauer der Schwingungen liegt ca. eine Zehnerpotenz über der des Rotierenden Abreißens. Pumpen tritt je nach Verdichterdruckverhältnis und Verbrauchervolumen mehr oder weniger stark auf. Tiefes Pumpen ist eine meist rotationssymmetrische Erscheinung mit großen Änderungen im Massenstrom; der Verdichter wird dabei periodisch in umgekehrten Richtungen durchströmt. Mildes Pumpen ist mit Oszillationen geringeren Ausmaßes verbunden. Es tritt zusammen mit Rotierendem Abreißen auf. Zu Rückströmungen kommt es nicht.

Einzelheiten zur Physik dieser Erscheinungen können z.B. bei Greitzer [11], Lindner [12] oder Traupel [13] nachgelesen werden. Alle Formen der Strömungsinstabilität sind durch einen einheitlichen Entstehungsmechanismus gekennzeichnet. Ist die maximale aerodynamische Belastung eines Schaufelgitters erreicht, löst die Strömung zunächst an einer Stelle am Umfang ab. Der hierdurch hervorgerufene höhere Strömungswiderstand zwischen zwei Schaufeln bewirkt, daß die Strömung in die in Umfangsrichtung benachbarten Schaufelkanäle ausweicht. Der Inzidenzwinkel zu den Profilen steigt zu einer Seite hin an, wodurch eine Fortbewegung des Ablösegebietes eingeleitet wird. In entgegengesetzter Richtung führt die Abnahme des Inzidenzwinkels zum Wiederanlegen der Strömung. Das so entstandene, sich fortpflanzende Ablösegebiet verursacht Rückwirkungen auf das gesamte Strömungsfeld, und die Wechselwirkungen zwischen den Druck- und Trägheitskräften innerhalb der Strömung entscheiden dann, welche Instabilitätsform das Leistungsverhalten des Verdichters verändert.

Für den Ingenieur ist indessen weniger wichtig, welche dieser Erscheinungen für seinen Verdichter in Frage kommen könnte, ob also z.B. nur Rotierendes Abreißen auftritt oder ob es zeitgleich mit dem Pumpen einsetzt oder auch zeitversetzt. Alle Erscheinungen stellen eine große Gefahr für den Betrieb dar und müssen vermieden werden. Sie liegen jenseits der Stabilitätsgrenze, die das Kennfeld eines jeden Verdichters zu kleineren Massenströmen hin abgrenzt.

Die Stabilitätsgrenze läßt sich wegen der komplizierten Strömungsverhältnisse im betrachteten Bereich nicht exakt vorhersagen. Vier halbempirische Kriterien, die zu ihrer Bestimmung vorgeschlagen werden und sämtlich für Gitter von Axialverdichtern gelten, nämlich das bisher bei Siemens eingesetzte Wirkungsgradkriterium sowie die Kriterien von Traupel [13], Lieblein [14] und Koch [15], werden nachfolgend erläutert und mit bekannten Pumpgrenzverläufen von Siemens-Verdichtern verglichen.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Modelle zur Bestimmung der Stabilitätsgrenze von Axialverdichtern

Bei Siemens wird zur Zeit mit einem Stabilitätsmodell gearbeitet, das als Wirkungsgradkriterium bezeichnet wird. Es gilt der Massenstrom als kritisch, bei dem die Kurve des isentropen Wirkungsgrades der Maschine für eine bestimmte Drehzahl ein Maximum aufweist. Diese Annahme, die darauf beruht, daß die beste Leistungsabgabe beim kleinsten abrißfreien Durchfluß liegen muß, ist jedoch nicht sehr genau. Bei Betrachtung von Kennfeldern mehrstufiger Verdichter, z.B. nach Lindner [12], [16], ist zu sehen, daß der Verlauf der Linie des maximalen Wirkungsgrades je nach Verdichtertyp mehr oder weniger weit rechts von der Stabilitätsgrenze liegt. Jedenfalls befindet man sich mit dem Wirkungsgradkriterium auf der sicheren Seite, wenn man damit die Betriebsgrenze eines Verdichters beschreiben will. Für die vorliegende Arbeit sind die Wirkungsgraddaten insofern von Bedeutung, als damit die Genauigkeit der zu überprüfenden Modelle beurteilt werden kann.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Äquivalente Diffusionszahl nach Lieblein

Die Analyse der reibungsbehafteten Profil- und Gitterströmung zeigt, daß die Grenzschichtentwicklung und insbesondere auftretende Grenzschichtablösungen das Verlust- und Umlenkverhalten der Schaufelgitter maßgeblich beeinflussen. Dies gilt insbesondere für Verzögerungsgitter, bei denen die Grenzschicht einen entsprechenden Druckanstieg überwinden muß.

Deshalb ist immer wieder versucht worden, geeignete Kriterien für eine einfache zahlenmäßige Abschätzung der Gitterbelastung (Umlenkung, Verzögerung, Druckanstieg) zu finden, die einem Schaufelgitter maximal oder optimal zugemutet werden kann. Zu ihnen zählen das de Haller-Belastungskriterium v2/v1, die Belastungszahl cA·σ, verschiedene Zirkulationszahlen oder auch die im Abschnitt 3 bereits erwähnte Diffusionszahl D in Gleichung (3.1) nach Lieblein.

Lieblein hatte bei Untersuchungen an ebenen Gittern festgestellt, daß die Impulsverlustdicke im Gitternachlauf im wesentlichen proportional zur Verzögerung auf der Profilsaugseite ist. Da aber die Maximalgeschwindigkeit auf der Saugseite im allgemeinen nicht bekannt ist, wurde versucht, D mit Hilfe von Korrelationsformeln wie z.B. Gleichung (3.2) zu erfassen, wobei hier nochmals erwähnt sei, dass Gleichung (3.2) nur für den Bereich minimaler Profilverluste zutrifft. Eine Ablösung der Strömung von der Saugseite der Schaufeloberfläche entsteht dann, wenn D folgende Grenzwerte überschreitet [4]:

D = 0,6 für die Kernströmung und den Nabenbereich des Laufrades
D = 0,48 im Naben- und Gehäusebereich des Leitrades
D = 0,45 im Gehäusebereich des Laufrades

Neben diesen Richtwerten für den Auslegungszustand entwickelte Lieblein einen verbesserten Belastungsparameter, der auch bei Anströmzuständen, die vom Referenzzustand minimaler Verluste abweichen, eine sinnvolle Korrelation mit der Impulsverlustdicke an der Schaufelhinterkante ermöglicht. Es ist dies die sogenannte äquivalente Diffusionszahl Deq.

Sie ist definiert als

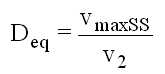Gleichung 5.1 (5.1)

und kommt dem reziproken Wert der de Hallerzahl (v2/v1) ziemlich nahe, ist allerdings schon deswegen günstiger, weil sie die Physik des Abrisses exakter beschreiben kann. Das erfordert natürlich die Kenntnis des Geschwindigkeitsverlaufes über der Schaufel. Die Korrelation, die Lieblein in [14] zur Berechnung von Deq angibt, lautet für NACA65 - (A10) Profile

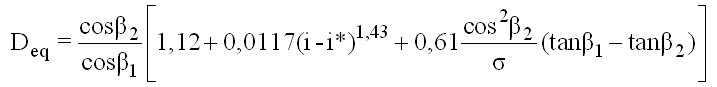Gleichung 5.2 (5.2)

Hierbei folgt cosβ2/cosβ1 wieder aus v1/v2.

Ausgewertet wurden Meßergebnisse einer Vielzahl von ebenen Gittern, bei denen Anströmwinkel, Umlenkung und Schaufeldichte variiert worden sind. Lieblein zeigt, daß ab Deq > 2 die Profilverluste stark ansteigen.

Betrachtet man die Gleichung (5.2), so sieht man, daß Lieblein neben dem Auslegungsinzidenzwinkel i* auch größere Inzidenzwinkel i zuläßt. Hierdurch werden Strömungen erfaßt, die im Bereich zwischen optimaler Zuströmung und Abriß liegen. Teillastzustände können also berücksichtigt werden. Es fällt auf, daß die Zuströmwinkel von großem Einfluß auf die Liebleinkorrelation sind. Auf die Entwicklung der Gleichung (5.2) geht Lieblein in seiner Arbeit nicht ein. Indessen erläutert er die Beziehung zwischen Diffusionszahl und Impulsverlustdicke, wobei letztere bei hohen Werten auf Abriß schließen läßt. Die Herleitung beruht auf der Anwendung der Kármán'schen Impulsgleichungen für die Schaufelgrenzschichten.

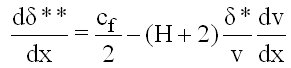Gleichung 5.3 (5.3)

Es wird eine zweidimensionale inkompressible Strömung vorausgesetzt; v ist die Geschwindigkeit am Grenzschichtrand.

Mit der Integration der Gleichung (5.3) von Gittereintrittskante bis Gitteraustrittskante erscheint auf der linken Seite die Impulsverlustdicke am Austritt in der Form δ**/s (es wird angenommen, daß Skelettlinie und Sehne identisch seien). Aus dv/v wird der Term ln(vmax/v2), was Gleichung (5.1) praktisch wiedergibt; vmax soll dicht am Eintritt liegen. Aus cf/2 wird ein integraler Wert gebildet und der Rest der Gleichung (5.3) vereinfachend, und zwar Glied für Glied gemittelt.

Nach diesen zum Teil groben Annahmen geht Lieblein zur Analyse einzelner Glieder und Abschätzung ihrer Größenordnung über. Er stellt fest, daß eine größere Umlenkung bzw. größere Zuströmwinkel zu starken Geschwindigkeitsgradienten auf der Saugseite führen, während die auf der Druckseite ohnehin schwachen Gradienten sich kaum ändern. Seine Betrachtungen, die in [6] ausführlich dargelegt sind, führen zur exponentiellen Abhängigkeit zwischen δ**/s und vmaxSS/v2

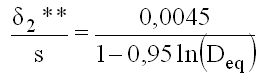Gleichung 5.4 (5.4)

und zur Bestimmung der Verlustzahl als

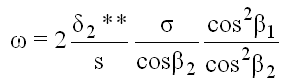Gleichung 5.5 (5.5)

Gleichung (5.4) und Gleichung (5.5) sind einer neueren Arbeit von Casey [17] entnommen. Sie weichen etwas von den ursprünglichen Formeln Liebleins ab, denn dieser gibt statt 0,0045 nur den Bereich 0,004 - 0,005 und statt 0,95 den Bereich 1 - 1,17 an. Die Verlustzahl multipliziert Lieblein noch mit dem Term 2H/(3H+1), was bei seiner Vorgabe von H = 1,08 = const. einen Faktor von 0,96 ergibt.

Will man Deq als Stabilitätskriterium für Verdichterstufen einsetzen, so kann die Korrelation nur Gitter für Gitter und Stromlinie für Stromlinie durchgeführt werden. Ähnlich wie bei D steht auch hier wieder die Frage, in wie weit die Berechnungsformel auf die Randzonen angewandt werden darf und ob hier der kritische Wert Deq = 2 überhaupt gültig ist. Leider wurden zu diesem Problem keine Veröffentlichungen gefunden.

Erfahrungen zeigen, daß lokale Überlastungen, also Überschreitungen von Deq = 2, zulässig sein müssen, denn bei stabilen Massenströmen kommt auch örtlich Deq > 2 vor. Traulsen [18] verlangt als Abrißbedingung für ein Gitter, daß über 30% der Schaufelhöhe Deq > 2 sein muß. In der vorliegenden Arbeit wird das Liebleinkriterium in ähnlicher Weise behandelt: die Stabilitätsgrenze des Verdichters gilt dann als überschritten, wenn für ein Gitter auf mehr als einem Drittel der Stromlinien Deq > 2 ist. Der dabei zugrunde liegende Massenstrom wird als jenseits der Stabilitätsgrenze bewertet.

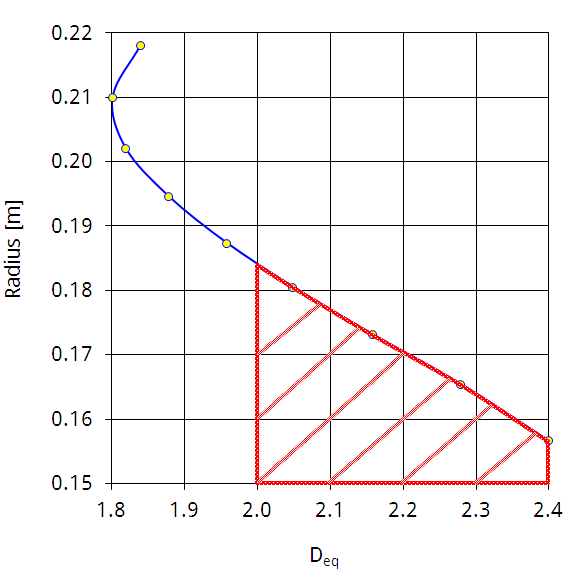
Abbildung 5.1: Beispiel für den Verlauf der äquivalenten Diffusionszahl über dem Radius eines Leitrades

Abbildung 5.1 verdeutlicht anhand eines ausgewählten Gitters, wie sich Deq über dem Radius eines Leitrades ändert. Die gerechneten Stromlinien sind durch Punkte hervorgehoben. Der Bereich, in dem Deq nach Lieblein zu groß ist, wurde schraffiert dargestellt. Die Nabe ist am stärksten belastet, was nach Liebleins Vorgaben meist zutreffen wird. Im vorgestellten Falle ist fast die halbe Schaufelhöhe überlastet. In vier von neun Stromlinien wird das Liebleinkriterium überschritten. Der dabei anliegende Massenstrom wird deshalb als instabil bewertet.

Bei Anwendung des Liebleinkriteriums kann es bei einzelnen Gittern und insbesondere bei größeren Massenströmen vorkommen, daß der Inzidenzwinkel kleiner wird als sein Referenzwert. Physikalisch treten dadurch Rückenanströmungen anstelle von Bruststößen auf und es kann zur Ablösung auf der Druckseite kommen. Damit sind zwar keine Instabilitäten wie die in Abschnitt 4 beschriebenen verbunden, dennoch kann die Strömung ein Schaufelflattern verursachen, das zu Ermüdungsbrüchen führt. Weil solche Zuströmbedingungen nicht über Deq erfaßbar sind, kann programmintern nur mit dem Referenzinzidenzwinkel als aktuellem Wert weitergerechnet werden. Die betroffenen Ergebnisse sind durch ein negatives Vorzeichen in der Ausgabedatei kenntlich gemacht. Große negative Werte sollten nicht unbeachtet bleiben, denn sie dokumentieren eine hohe Gitterbelastung selbst bei optimaler Zuströmung.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Methode der radialen Stufenelemente nach Traupel

Abweichend von Lieblein verlangt Traupel, daß zur Beurteilung der Stabilität die Stufe als ganzes betrachtet werde. Dazu führt er in [13] die Stokesche Stromfunktion Ψ ein, mit deren Hilfe er die Stufe radial in einzelne Elemente zerlegt. Ψ kann theoretisch die Werte von 0 bis 1 annehmen, denn es charakterisiert den Anteil des Massenstromes bis zu einer festgelegten Stromlinie am Gesamtmassenstrom. Ψ = 0 kann somit für die Nabe und Ψ = 1 für das Gehäuse definiert werden. Entlang der Linien Ψ = const., also der einzelnen Stromlinien oder Stufenelemente betrachtet Traupel nun die Charakteristik des Enthalpieanstieges innerhalb der gesamten Stufe über dem Durchfluß in der dimensionslosen Abhängigkeit der Druckzahl ψ über der Durchflußzahl φ, wobei sich ψ und φ auf eine feste Umfangsgeschwindigkeit, z.B. die im Mittelschnitt beziehen. φ wird mit der Geschwindigkeit am Laufradaustritt berechnet. Unmittelbar wandnahe Schichten (Ψ < 0,1 und Ψ > 0,9) gehen in die Betrachtung nicht ein.

Traupel untersucht nun eine Stufe, bei der sich der Arbeitsumsatz über dem Radius für den jeweiligen Massendurchsatz kaum ändert. Zur Erläuterung dient die Abbildung 5.2.

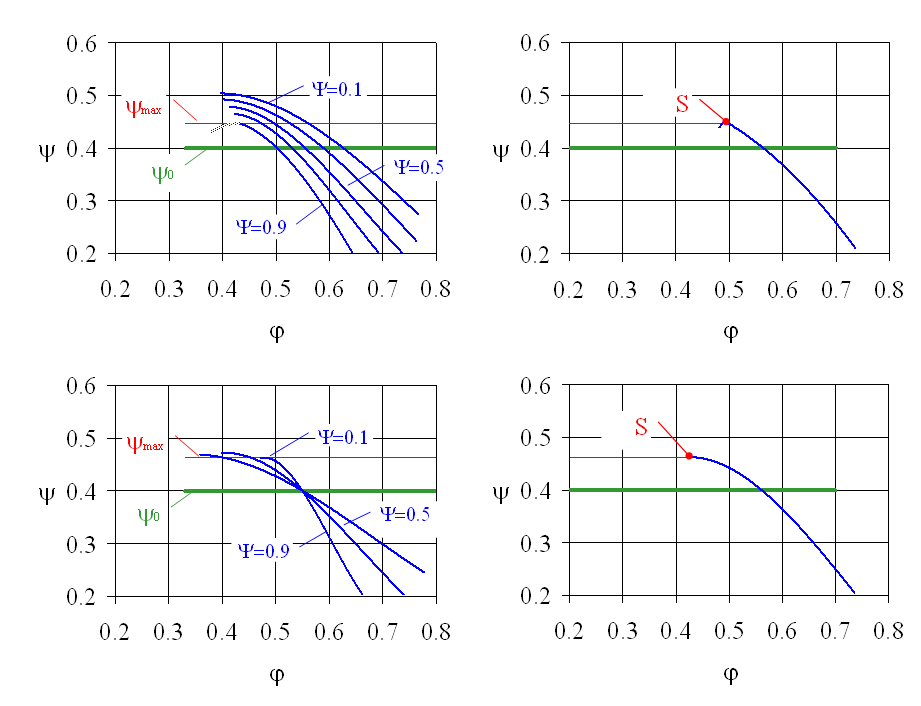
Abbildung 5.2: Kennlinien der einzelnen Stufenelemente und gesamte Stufencharakteristik von Axialverdichterstufen nach Traupel

Nach seiner Forderung gilt für alle Stufenkennlinien bei einem vorgegebenen Massenstrom: ψ(r) ≈ const.

Jede Stufenkennlinie wird bei irgendeinem separaten Durchsatz ein Maximum aufweisen, das heißt die Kurve hat eine waagerechte Tangente. Bei irgendeiner der Kurven liegt dieses (separate) Maximum am tiefsten. Dieses Maximum legt die Stabilitätsgrenze der gesamten Stufe fest. Wird in dem kritischen Stufenelement der Durchsatz, der dem Kennlinienmaximum entspricht, unterschritten, so bricht dort die Strömung zusammen, weil die durch die übrigen Stufenelemente aufgezwungene Druckerhöhung größer ist, als nach der Kennlinie des betreffenden Elements erzeugt werden kann.

Das kritische Maximum befindet sich im Gegensatz zum Liebleinkriterium häufig außen, was Traupel damit begründet, daß dort die Verluste bei Fehlanströmungen der hohen Machzahlen wegen besonders stark ansteigen. Weiterhin liegt der zulässige Grenzwert für die Diffusionszahl, wie in 5.1 angedeutet, außen tiefer.

Aus der Schar der Kennlinien der einzelnen Stufenelemente gewinnt Traupel jetzt die integrale Darstellung von ψ über φ. Weil sich die ψ über der Schaufelhöhe kaum ändern, kann er anhand des ermittelten kritischen separaten ψ das integrale φ bestimmen, welches den Massenstrom an der Stabilitätsgrenze für die vorgegebene Drehzahl repräsentiert.

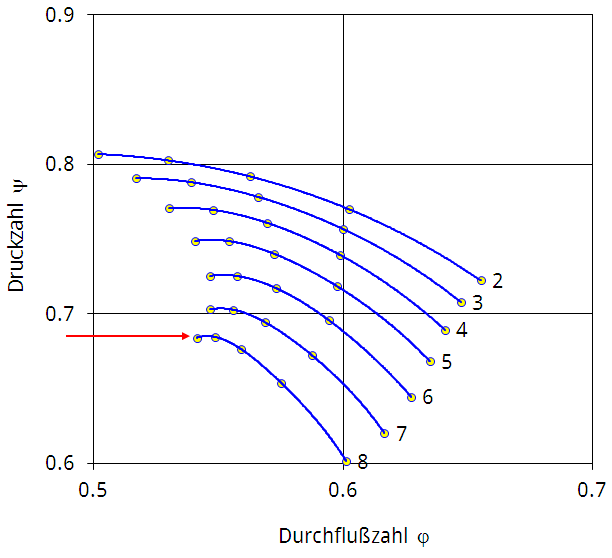
Abbildung 5.3: Separate Kennlinien für eine untersuchte Verdichterstufe

Abbildung 5.3 zeigt eine Darstellung separater Kennlinien, also der für die einzelnen Stufenelemente, wie sie sich nach einer Kennlinienrechnung für die letzte Stufe eines vierstufigen Siemens-Versuchsverdichters ergibt. Die Strömungsverhältnisse sind auf neun Stromlinien berechnet. Die Ziffern zwei bis acht an den dargestellten Linien geben die Nummern der bei der Auswertung berücksichtigten Stromlinien an. Die Stromlinien direkt an Nabe und Gehäuse fallen also bei der Untersuchung heraus. Auf jeder Kennlinie sind fünf Punkte besonders hervorgehoben. Sie verdeutlichen die fünf gerechneten Massenströme (22,2 bis 23,0 kg/s). Die Rechnung gilt für Nenndrehzahl.

Das Beispiel zeigt, daß mehrere Kennlinien bei kleinen Massenströmen ein Maximum aufweisen, wobei das Maximum des äußersten Stufenelements absolut am tiefsten liegt, was Traupel auch erwartet. Dieses kleinste lokale Maximum der Druckzahlen in Abbildung 5.3 liegt bei ψ = 0,68, was bedeutet, daß das Stufenelement keinen höheren Druckanstieg verwirklichen kann als eben diesen, der 0,68 entspricht. Die einzelnen Kennlinien haben bei gleichem Gesamtmassenstrom leider sehr unterschiedliche ψ. Als Auslegungsgesetz der Stufe ist demnach nicht die Potentialwirbel-drallverteilung genommen worden. Die großen Unterschiede in ψ über r bedeuten aber auch, daß Traupels Vorgehensweise nicht zum richtigen Ergebnis führen würde, wenn man das Beispiel aus Abbildung 5.3 danach analysieren wollte.

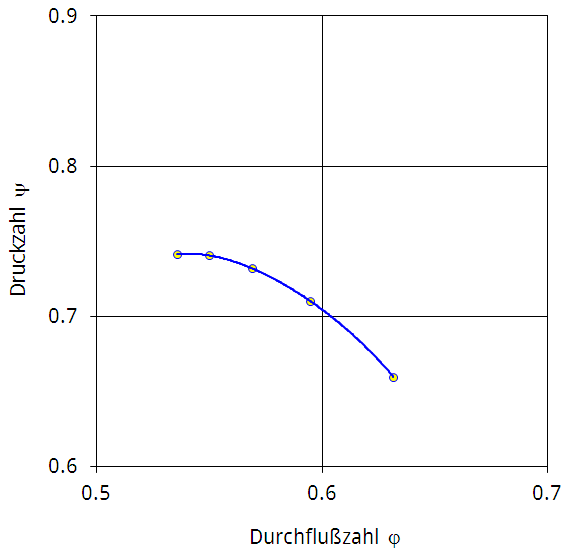
Abbildung 5.4: Integrale Kennlinie für die untersuchte Verdichterstufe aus Abbildung 5.3

Abbildung 5.4 stellt zur Veranschaulichung die integrale Kennlinie dar, die durch Massenstrommittlung der ψ und φ aus Abbildung 5.3 gewonnen werden kann. Es fällt sofort auf, daß das kritische φ zwischen Betriebspunkten liegt, für die die separaten Kennlinien keine Instabilitäten andeuten. Rechnerischer Grund dafür ist, daß das ψ von 0,68 integral gesehen natürlich erst bei viel größeren Massenströmen erreicht wird.

Es wäre sicher nützlich, das Stabilitätskriterium für eine nach Traupels Anforderungen ausgelegte Maschine zu testen; umso mehr als er sein Postulat durch keine experimentellen Vergleiche bestätigt.

Für die vorliegende Maschine ist nur die Wahl geblieben, das Traupelkriterium außer Acht zu lassen oder zu modifizieren. Für den Verdichter aus Abbildung 5.3 liegt die tatsächliche Stabilitätsgrenze zwischen den beiden Massenströmen, innerhalb derer sich auch der kritische Druckanstieg ergibt. Deshalb hat sich der Autor zu folgender Vorgehensweise entschlossen.

Aus der Lage des kritischen ψ wird das separate φ durch Interpolation über der entsprechenden Kennlinie gebildet. Dieses charakterisiert einen bestimmten Gesamtmassenstrom, welcher ebenso durch Interpolation aus den vorgegebenen Massenströmen bestimmbar ist. Der auf diese Art ermittelte Massenstrom wird für sämtliche Stufen verglichen. Der größte sich so ergebende Wert gilt, gleich welche Stufe er betrifft, als der für die Stabilitätsgrenze des gesamten Verdichters charakteristische.

Natürlich ist dieser Weg nicht exakt. Es läßt sich im Einzelfall schwer sagen, ob für das kritische Element zu hohe Druckanstiege, nicht doch von anderen Elementen mit steilen Kennlinien übernommen werden können. Andere Fälle sind ebenfalls möglich, denn anhand von Nachrechnungen läßt sich zeigen, daß sämtliche Kennlinien für alle Stufen bis weit in den instabilen Bereich monoton ansteigen können.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Diffusormodell von Koch

Betrachtet man einen Schaufelkanal innerhalb eines Verdichters, so arbeitet dieser quasi als Diffusor. Durch Querschnittserweiterung des Kanals wird die Strömung unter Druckanstieg verzögert. Der erreichbare Druckanstieg läßt sich für einen Diffusor aus seiner vorgegebenen Geometrie ermitteln, wozu man Kennfelder wie die von Albring [19] oder Sovran und Klomp [20] (s. a. Abbildung 5.5) verwenden kann. Hier ist das Flächenverhältnis über Diffusorlängen, bezogen auf die Eintrittsbreite, aufgetragen. Im Kennfeld werden Linien gleichen statischen Druckanstiegs dargestellt. Die Werte gelten immer nur für eine festgelegte Dicke der Eintrittsgrenzschicht, denn von ihr ist der mögliche Druckanstieg abhängig. Im Beispiel sind es 5% Blockierung am Eintritt, was bedeutet, daß der Strömungsquerschnitt aufgrund der Verdrängungsdicke um 5% kleiner ist als der geometrisch vorgegebene. Wichtig ist noch die experimentell ermittelte Kurve, die für eine gegebene bezogene Diffusorlänge das Flächenverhältnis angibt, bei dem der statische Druckanstieg maximal wird. Wird das Flächenverhältnis weiter vergrößert, so ergibt das nur einen größeren Anteil an abgerissener Strömung bei gleichem oder sogar kleinerem Druckanstieg.

Abbildung 5.5: Diffusor-Analogie für Verdichterschaufeln - Bild links © ASME [15]

Koch versucht, diese Erfahrungen auf Verdichter zu übertragen. Dabei stellt er als erstes fest, daß sich für seine Anwendung das Flächenverhältnis nicht allein aus der Schaufelgeometrie ergibt. Dieses wird zum Beispiel größer, wenn die Strömung zu höheren Inzidenzwinkeln und kleineren Durchflußzahlen hin gedrosselt wird. Was sich bei unterschiedlichen Drosselzuständen allerdings kaum ändert, ist die senkrecht durchströmte Austrittsfläche. Hieraus folgt zweierlei.

Zum einen muß als unabhängiger Abszissenparameter eine Strömungskanallänge, bezogen auf eine Austrittsbreite gebildet werden.

Zum zweiten muß sich aus dieser Größe und nicht etwa aus dem Flächenverhältnis der maximal mögliche Druckanstieg bestimmen lassen, der ja gleichzeitig die Grenze des stabilen Arbeitsbereiches darstellt.

Diese Überlegungen bilden die Grundlage für die Diffusoranalogie Kochs in [15]. Koch stellt dort schließlich auch eine Kurve (siehe Abbildung 5.6) vor, die für die vorgegebene Geometrie einer Verdichterstufe vorhersagen kann, welcher Druckanstieg bzw. welcher Enthalpieanstieg in ihr erreichbar ist. An physikalischen Größen sind nur wenige Mittelschnittdaten erforderlich, was den Vorteil dieses Modells für Vorentwurfsphasen neuer Stufen hervorhebt. Kochs Verfahrensweg soll nachfolgend beschrieben werden.

Abbildung 5.6: Koch'sche Korrelation für die Stabilitätsgrenze © ASME [15]

Als Abszissenparameter wird die Länge l der kreisbogenförmigen Skelettlinie einer Schaufel gewählt, welche auf die Schaufelkanalweite am Austritt g2 bezogen wird. Weil Koch seine Betrachtungen immer auf gesamte Stufen bezieht, mittelt er die Werte von l/g2 aus Laufrad und Leitrad und wichtet sie mit den kinetischen Energien am jeweiligen Gittereintritt.

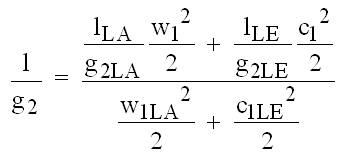Gleichung 5.6 (5.6)

In Abbildung 3.1 sind die Formeln angegeben, nach denen sich l und g2 ermitteln lassen.

Kochs Stabilitätskriterium ist nun ein Enthalpiekoeffizient Ch, der sich aus der statischen Enthalpieerhöhung der Stufe entlang der Isentropen ergibt. Enthalpieänderungen, die durch unterschiedliche Umfangsgeschwindigkeiten auf der Stromlinie am Ein- und Austritt des Laufrades bedingt sind, werden davon abgezogen, denn sie haben mit der Physik des Abreißens der Strömung nichts zu tun. Der sich ergebende Wert wird, ebenso wie l/g2, auf die kinetischen Energien am Eintritt bezogen.

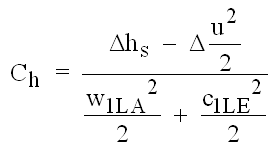Gleichung 5.7 (5.7)

Die Verdichter, die Koch in seine Stabilitätsuntersuchungen einbezieht, haben unterschiedlichste Daten.

Nabenverhältnis am Eintritt von 0,40 bis 0,92
l/g2 von 0,65 bis 3,5
Machzahlen am Eintritt von 0,1 bis 1,6
Reaktionsgrade von 0,4 bis 1,1
Seitenverhältnisse (aspect ratios) h/s von 0,35 bis 5,0
Gitterdichten s/t von 0,6 bis 3,0
Staffelungswinkel von 22° bis 51°
Wölbungswinkel von 31° bis 36°
Radialspiele von 0,7 bis 3,4% der Schaufelhöhe
Stufenzahlen bis hoch zu 16

Koch versucht, die Funktion Ch(l/g2) in gute Übereinstimmung mit der Sovran/Klomp Korrelation zu bringen. Er zeigt, daß seine Daten für die Sovran/Klomp Kurve bei 9% Blockierung am Eintritt die beste Genauigkeit erzielen (Abbildung 5.6). Dennoch ist der Streubereich groß, was Koch mit unterschiedlichen Reynoldszahlen (gebildet aus Eintrittsgeschwindigkeit und Sehnenlänge des Laufrades) sowie verschiedenen Radialspielen und Axialspalten bei den einzelnen Verdichtern begründet. Abbildung 5.7, Abbildung 5.8 und Abbildung 5.9 zeigen die interpolierten Korrekturfunktionen f1, f2 und f3. Die Funktionen werden verwendet, um das ermittelte Ch auf bestimmte Bezugswerte umzurechnen:

f1 → Reynoldszahl Re = 1,3·10⁵
f2 → Radialspiel ε/g = 0,055
f3 → Axialspalt Δz/t = 0,3

Es wird der Quotient gebildet. Hiernach liegen die Pumpgrenzpunkte schon in einem engeren Bereich der Sovran/Klomp Kurve aus Abbildung 5.6.

Abbildung 5.10 zeigt die interpolierte Vergleichsfunktion zur Abbildung 5.6.

Das Auswerteprogramm benutzt die Korrekturfunktionen und nähert sich den veröffentlichten Kurven von Koch mit Polynomen vierten Grades an. Vergleichspunkte aus den veröffentlichten Kurven sind in den Abbildungen besonders gekennzeichnet. Die angezeigten Polynomkoeffizienten in den Abbildungen sind gerundet. Die exakten Koeffizienten können im Programmlisting nachgeschlagen werden.

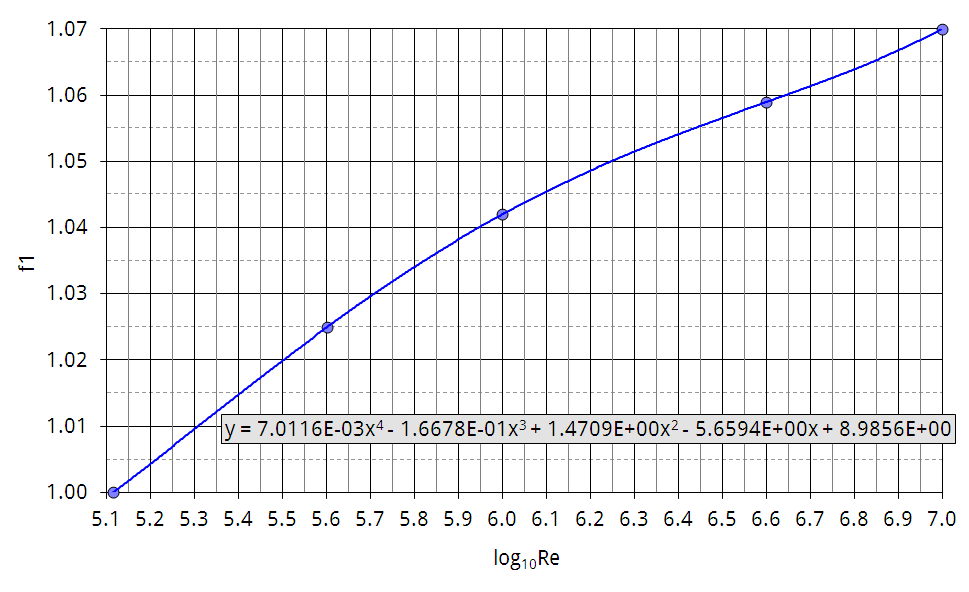
Abbildung 5.7: Korrekturfunktion für die Reynoldszahl als Polynom 4. Grades

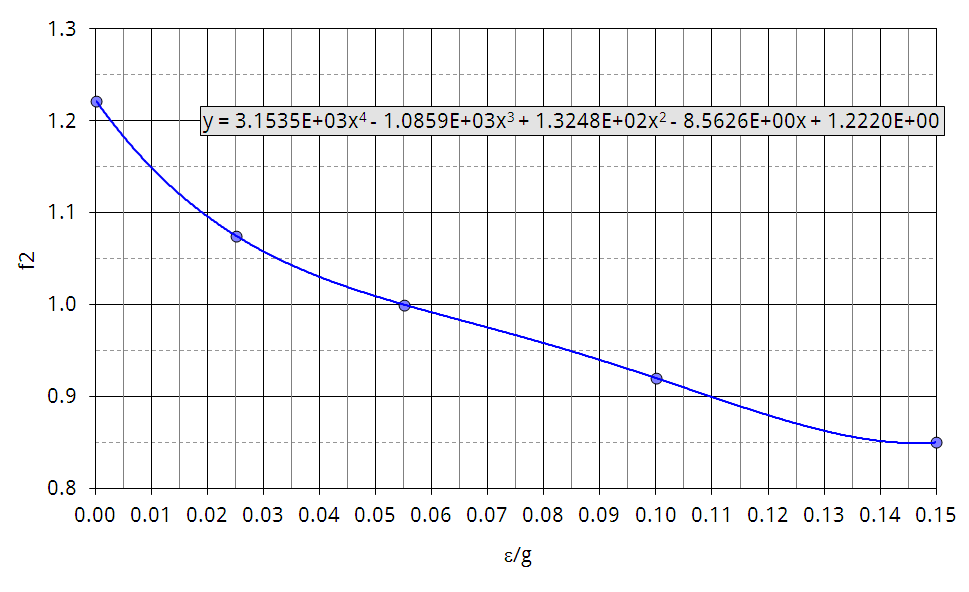
Abbildung 5.8: Korrekturfunktion für die Radialspiele als Polynom 4. Grades

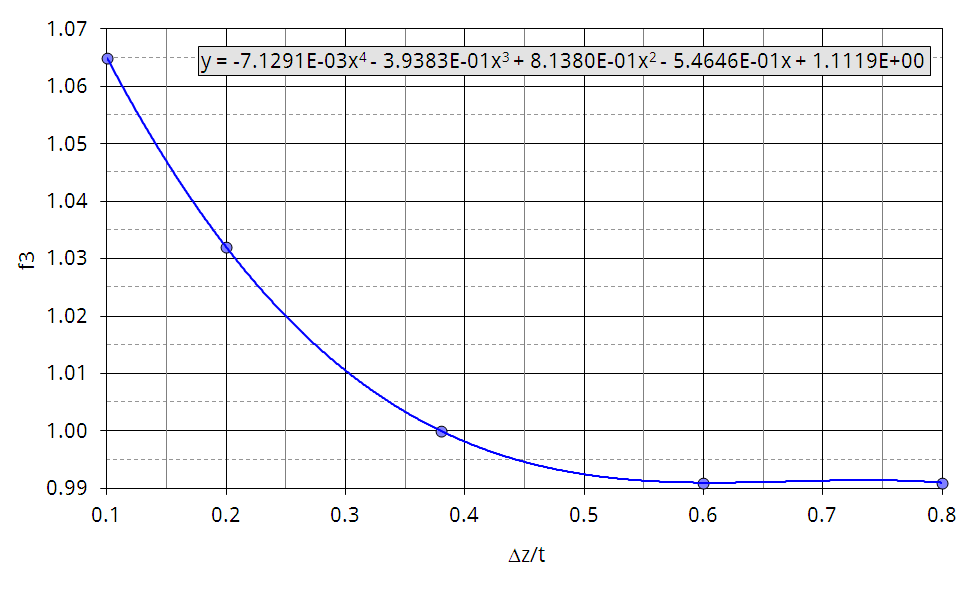
Abbildung 5.9: Korrekturfunktion für die Axialspalte als Polynom 4. Grades

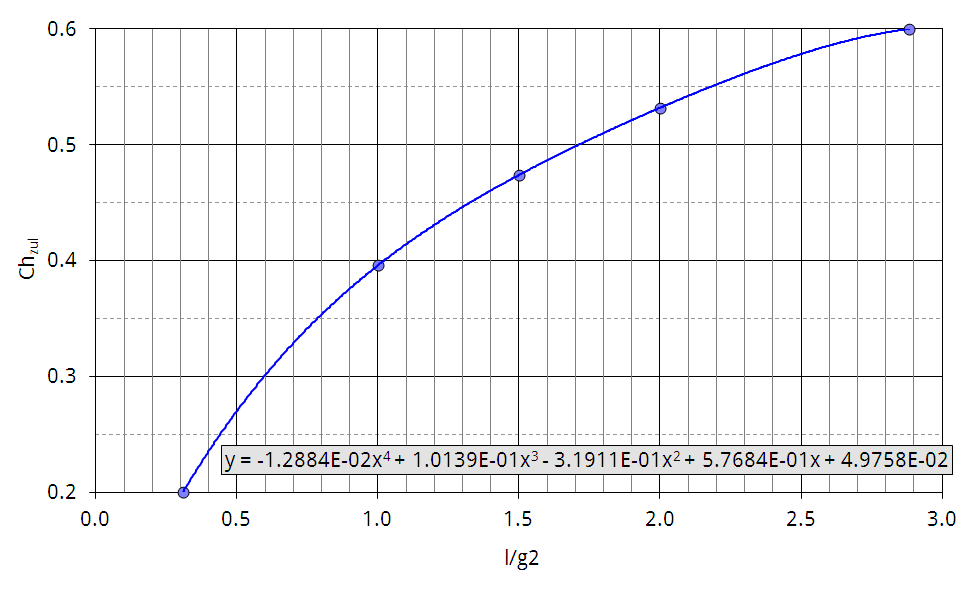
Abbildung 5.10: Vergleichsfunktion zur Abbildung 5.6 als Polynom 4. Grades

Für den Autor haben sich bei den Kochkorrekturen folgende Schwierigkeiten ergeben:

Die Reynoldszahlen der untersuchten Verdichter liegen deutlich über denen, die Koch in seiner Korrektur berücksichtigt. Der Funktionsverlauf ist deshalb mittels Kurvenschablone soweit verlängert worden, daß er auch den Bereich von 106 bis 107 überstreicht. Wegen des hohen Grades des gebildeten Polynoms nimmt dabei der Anstieg der Funktion in diesem extrapolierten Bereich leider wieder etwas zu. In der Realität dürfte er weiter abnehmen; allein der Unterschied hat minimale Auswirkungen, wie an den Korrekturfaktoren in dem Bereich zu sehen ist.
In der Dynatech Rechnung tauchen keine Radialspiele auf. Vereinfachend rechnet das Programm STAB an dieser Stelle mit der Annahme weiter, daß das Spiel 1% der Schaufelhöhe beträgt.
Auf Axialspalte kann nur über die Eingabedatei zur Dynatech Rechnung zurückgegriffen werden, was bedeutet, daß etwaige Leitschaufelverstellungen unbeachtet bleiben.
Die Bezugsgröße von Kochs Korrekturfunktion für die Radialspalte ist nicht eindeutig erklärt. Er bezieht das Radialspiel ε des Laufrades auf eine mittlere Kanalbreite g, ohne diese näher zu beschreiben. Das Programm STAB mittelt deshalb g2 von Lauf- u. Leitrad.

Koch gibt noch eine letzte Korrektur für Ch an, die sich daraus ergibt, daß bei kleinen Staffelungswinkeln der mögliche Enthalpieanstieg kleiner ist als bei großen, was sich mit der Diffusoranalogie nicht erklären läßt. Dieser qualitativ neue Effekt hängt mit der Fähigkeit oder Unfähigkeit einer Stufe zusammen, einer Grenzschichtströmung mit schwachem Impuls beim Wechsel des Bezugssystems wieder Energie zuführen zu können. Zur Veranschaulichung des Problems, das nur auf Turbomaschinen zutrifft, dient die Abbildung 5.11.

Abbildung 5.11: Korrekturfaktor Fef für die kinetischen Energie [15] © ASME [15]

Mit durchgehenden Linien ist das Geschwindigkeitsdreieck eingezeichnet, daß sich zwischen Laufrad und Leitrad in der Kernströmung ergibt. Für die Grenzschichtströmung, welche das Laufrad mit dem gleichen Winkel β verlässt wie die Kernströmung, kann das Geschwindigkeitsdreieck im Gitternachlauf ganz anders aussehen. Die Absolutgeschwindigkeit ist hier reduziert, der Winkel α dabei gleichzeitig vergrößert. Je größer der relative Impulsverlust im Laufrad ist, desto größer wird α. Der Impuls der auf das Leitrad auftreffenden Strömung sinkt unterdessen bis zu einem Winkel αmin ab, wie in der Abbildung zu sehen ist. Dieser Punkt tritt genau dann ein, wenn αmin+β = 90°. Bei noch größeren Verlusten als denen, die zu αmin führen, würde der absolute Impuls wieder größer werden und sich der Umfangsgeschwindigkeit u annähern.

Stufen, die große Durchflußzahlen und kleine Staffelungswinkel aufweisen, haben die Eigenschaft, daß die Absolutgeschwindigkeit cmin viel kleiner ist, als das c der Kernströmung, wenn α+β << 90° ist. Der erreichbare dynamische Druck tendiert durch die impulsschwache Strömung zu sehr kleinen Werten. So läßt sich erklären, daß eben beschriebene Stufen unter sonst gleichen Bedingungen viel abreißgefährdeter sind als andere. Umgekehrt können Stufen mit großem Staffelungswinkel und kleinen Durchflußzahlen durchaus einen Impulsgewinn für die Grenzschichtströmung erzielen, wodurch die Abreißgefahr sinkt.

Kochs letzte Korrektur betrifft deshalb die Analyse der Geschwindigkeitsdreiecke und die Berücksichtigung der minimalen Geschwindigkeit, die im neuen Bezugssystem auftreten kann. Die kinetischen Energien am Eintritt werden durch diese Funktion, die er mit Fef bezeichnet, in effektive kinetische Energien umgerechnet. Im Nenner von Gleichung (5.7), die die Berechnung von Ch zeigt, ist das zu berücksichtigen. Beide dynamischen Enthalpien in Gleichung (5.7) müssen mit dem entsprechenden Fef multipliziert werden. Wie Fef zu ermitteln ist, kann am Beispiel des Leitrades in Abbildung 5.11 gesehen werden.

Bei der Beurteilung der Stabilität nach Koch wird wie folgt verfahren. Stufe für Stufe wird im Mittelschnitt l/g2 nach Gleichung (5.6) und Ch nach Gleichung (5.7) berechnet. Der Nenner von Ch wird mit Fef für Lauf- und Leitrad korrigiert. Anschließend werden die Korrekturen von Ch für die Reynoldszahlen und für die radialen Spiele des Laufrades sowie die axialen Spalte zwischen Lauf- und Leitrad durchgeführt. An dieser Stelle sei nochmals an die Einschränkungen erinnert, die weiter oben beschrieben sind. Schließlich wird aus l/g2 das zulässige Ch ermittelt und mit dem tatsächlichen Ch verglichen. Für jede Stufe kann Ch durch seinen zulässigen Wert dividiert und über dem Massenstrom aufgetragen werden. Mittels Interpolation wird dann der größte Massenstrom errechnet, bei dem der Quotient größer oder gleich eins ist. Der Vergleich sämtlicher Stufen ergibt danach den größten kritischen Massenstrom nach Koch.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Vergleich der Modelle

Alle drei Modelle weisen gewisse Gemeinsamkeiten auf. Sie bieten die Möglichkeit, in den Verdichter "hineinzugehen", so daß man nicht nur auf eine gerechnete Gesamtcharakteristik bei der Beurteilung der Stabilitätsgrenze angewiesen ist.

Traupel und Koch betrachten jeweils eine gesamte Stufe, wobei sich ihre Kriterien darin ähnlich sind, daß sie jeweils den isentropen Enthalpieanstieg untersuchen. Während Traupel direkt die Stufencharakteristik bewertet, korreliert Koch den Arbeitsumsatz mit einem Geometrieparameter.

Lieblein untersucht dagegen jedes Gitter für sich und verwendet dabei als kennzeichnenden Parameter die aerodynamische Gitterbelastung.

Lieblein und Traupel betrachten jeweils die radiale Verteilung ihrer Kenngröße und müssen lokale Überschreitungen besonders im Seitenwandbereich zulassen. Die hierbei zu treffenden Annahmen sind noch recht willkürlich und können durch systematisches Probieren gut an experimentelle Erfahrungen angenähert werden. Während sich aus Liebleins Vorstellungen ergibt, daß die Instabilität häufig von der Nabe ausgeht, führen Traupels Betrachtungen dazu, daß zumeist außen der kritische Bereich liegt.

Koch umgeht dieses Problem, denn er bewertet die Stabilität lediglich anhand von Mittelschnittdaten. Der Einfluß der Randzonen geht aber implizit in die Betrachtungen ein, die sich aus Meßdatenanalysen an unterschiedlichsten Verdichtern ergeben.

In Abschnitt 8 wird gezeigt, wie die Modelle im Vergleich zur tatsächlichen Stabilitätsgrenze von verschiedenen Verdichtern liegen.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Der Einfluß der Vielstufigkeit auf die Stabilitätsgrenze von Verdichtern

Es sei πR0 das Ruhedruckverhältnis eines vielstufigen Verdichters im Auslegungspunkt.

Wenn das Druckverhältnis unter πR0 sinkt, was z.B. bei niedrigeren Drehzahlen als der Nenndrehzahl eintreten kann, so nimmt die Dichte des Fluids weniger stark zu, weshalb die Durchflußzahl entlang der Maschinenachse ansteigt und schließlich, beginnend mit der letzten Stufe, die Schluckgrenze erreicht wird. Ein Betrieb jenseits der Stabilitätsgrenze kann nur durch die ersten Stufen verursacht werden, denn dort sind die Durchflußzahlen am kleinsten. Bei genügend kleinem Massenstrom fallen sie hier zuerst unterhalb des kritischen π, das die Stabilität der Stufe begrenzt.

Ist hingegen πR > πR0, so nimmt die Dichte entlang der Maschinenachse mehr zu als angestrebt. Die Durchflußzahl φ fällt deshalb wegen der Kontinuität bis zur letzten Stufe immer weiter ab und kann dort das die Stabilität abgrenzende π am ehesten unterschreiten. Für diesen Fall, der im Bereich größerer oder nur wenig kleinerer Drehzahlen als der Nenndrehzahl auftreten kann, wird die Stabilitätsgrenze ausgehend von der letzten Stufe bestimmt. Die Verschiedenheit der die Stabilität gefährdenden Stufen ist Ursache dafür, daß die Stabilitätsgrenze keinen gleichmäßigen Verlauf im Kennfeld eines vielstufigen Verdichters hat.

Tritt der zuerst beschriebene Fall ein, bei dem die vorderen Stufen eines Verdichters instabil werden, so ist es durchaus möglich, daß der Verdichter als ganzes trotzdem noch stabil fördert. Mechanikov [21] schreibt dazu weiter, daß die hinteren Stufen kaum Arbeit verrichten und so eine stabilisierende Wirkung auf das gesamte System ausüben. Bei kleineren Drehzahlen (ca. 0,3-0,4- faches der Nenndrehzahl) kommt es bei seinen Untersuchungen sogar zu solch großen Anstiegen von π, daß ein Druckabfall hervorgerufen wird und die letzten Stufen als Turbine arbeiten. Der beschriebene Druckabfall kann größer sein als der gesamte frühere Druckgewinn. Entnahmen nach den ersten Stufen wirken beim Anfahren stabilitätsfördernd. Zufällige Erregungen z.B. beim Öffnen von Ventilen zur Pumpgrenzverhütung oder beim Durchfahren bestimmter Drehzahlbereiche beeinträchtigen die Stabilität. Burmaskov [22] erwähnt Fälle, in denen ein Abreißen in der ersten Stufe beginnt und sich dann durch den gesamten Kompressor fortpflanzt. Entnahmen haben hier den abrißgefährdeten Drehzahlbereich verringert; Leitschaufelverstellungen sind kaum von Einfluß gewesen.

Suter/Späti [23] verwerfen die Vorstellung, daß sich Instabilitäten in den letzten Stufen eines Verdichters nicht mehr ausgleichen lassen und der Verdichter als ganzes instabil wird. Für höhere Betriebsdruckverhältnisse als denen im Auslegungspunkt ist das interessant. Sie schlagen als Pumpgrenzkriterium eine mittlere Durchflußzahl vor, welche sich aus Aufsummierung derer für die Stufen und Division durch die Stufenzahl ergibt. Für die verschiedensten Drehzahlen variiert dieser Wert nach Suter/Späti nur wenig.

Alle Fälle unterstreichen nur das Komplizierte des Systems und zeigen die Unzulänglichkeiten der in 5.1, 5.2 und 5.3 beschriebenen Methoden. Dort wird sofort der gesamte Verdichter als instabil bewertet, wenn in einem einzigen Gitter oder einer einzigen Stufe, gleich wo, das Kriterium versagt. Dieser Gesichtspunkt sollte in jedem Falle Beachtung finden. Rezepte, die diesen Mangel der untersuchten Modelle ausgleichen könnten, gibt es leider noch nicht. Mit der angewandten isolierten Betrachtung eines Gitters oder einer Stufe in einer mehrstufigen Umgebung dürfte man aber auf der sicheren Seite liegen.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Erläuterungen zum Programm STAB zur Bestimmung der Stabilitätsgrenze

Der Source Code zum Programm STAB ist im Anhang gelistet, gleichfalls die Prozedur PROC.STAB, über die das Programm gestartet wird, sowie ein Beispiel für die im Ergebnisfile $(NAME.TYP).STAB.DTA abgelegten Daten.

STAB läuft über eine Prozedur, da dadurch eine bequeme Dateiarbeit möglich ist. Es muß auf die Eingabedatei $(NAME.TYP) und die Ergebnisdatei $(NAME.TYP).PLOT einer Dynatech Rechnung zurückgreifen können. STAB setzt voraus, daß die Dynatech Rechnung erfolgreich, also ohne Abbruch, durchgeführt wurde. Eine sinnvolle Auswertung ist nur unter folgenden Bedingungen möglich.

Wenigstens drei Betriebspunkte müssen gerechnet worden sein. Liegt die Zahl der gerechneten Betriebspunkte über zehn, so werden nur die ersten zehn ausgewertet.
Sämtliche Punkte sollten bei gleicher Drehzahl liegen.
Die vorgegebenen Massenströme müssen entweder monoton fallen oder steigen und sollten in gleichen Abständen voneinander liegen.

STAB ist ein unabhängiges Fortranprogramm von wenigen Sekunden Laufzeit. Es wurde absichtlich nicht in die Dynatech Rechnung implementiert, um es besser von den vorgeschalteten Rechnungen abgrenzen und gegebenenfalls verändern zu können. Es enthält keine Sprunganweisungen und läßt sich so in seinem Ablauf gut "von oben nach unten" verfolgen. Sämtliche Größen sind eingangs erläutert. Das Programmlisting ist mit umfangreichen Kommentaren ausgestattet.

Es sei eine Dynatech Rechnung wie oben beschrieben durchgeführt worden. Zum Einsatz des Programms STAB muß der Nutzer als erstes die Prozedur mit

DO $TGMV.PROC.STAB

aufrufen. Anschließend wird mit

NAME

die Benutzerkennung abgefragt, unter der die Dynatech Dateien abgelegt sind. Das kann z.B. TGMV sein. Nachfolgend erscheint

TYP

auf dem Bildschirm, und hier muß der Name der Eingabedatei zur Dynatech Rechnung eingegeben werden.

Weitere Vorgaben sind nicht nötig.

Die Prozedur öffnet die Files $(NAME.TYP) und $(NAME.TYP).PLOT sowie eine weitere Datei $(NAME.TYP).STAB.DTA, in welcher die Ergebnisse aus STAB abgespeichert werden. Dazu zählen

Beschreibung des Verdichters
Beschreibung der Betriebspunkte
Aufführung der einzelnen Rechenebenen mit
- Stromliniennummer
- Stromlinienradius
- äquivalenter Diffusionszahl nach Lieblein
- Druckzahl und Durchflußzahl nach Traupel
- Enthalpiekoeffizienten nach Koch
isentroper Wirkungsgrad der Beschaufelung
kritische Massenströme, entsprechende Ruhedruckverhältnisse und Kurzbeschreibung der zugehörigen Ebenen

Zusätzlich werden temporäre Dateien #STAB.PLOT.1 bis #STAB.PLOT.17 eröffnet. Die Nummer gibt die Stufennummer an, für die die Datei bestimmt ist. Jede Datei enthält für ihre Stufe alle nach Traupel errechneten separaten φ und ψ. Über das bei Siemens vorhandene Grafikprogramm XYPLOT kann unter Vorgabe von z.B. #STAB.PLOT.1 das Kennfeld ψ(φ) für die separaten Stufenelemente der ersten Stufe sichtbar gemacht werden. Ein Beispiel dafür liefert die Abbildung 5.3 im Abschnitt 5.2.

Durch den LOGOFF-Befehl werden alle temporären Dateien gelöscht!

Jetzt zum eigentlichen Programm, das nach Eröffnung der Dateien gestartet wird.

Folgende Größen werden aus dem Ergebnisfile der Dynatech Rechnung übernommen:

Stationszahl je Stromline
Stromlinienanzahl
Zahl der Lauf-, Leit- und Vorleiträder
Zahl der Betriebspunkte

sowie für jeden Punkt

Gesamtdruckverhältnis
Massenstrom
Verhältnis der gerechneten Drehzahl zur Nenndrehzahl
Sehnenlängen an Nabe und Gehäuse
Radien der Stromlinien am Ein- und Austritt der Gitter
äquivalenter Schaufelwinkel am Austritt
Wölbungswinkel
aktueller sowie Referenzinzidenzwinkel
Axialgeschwindigkeit am Austritt
statischer Druck und statische Temperatur am Austritt
Zu- und Abströmwinkel der Strömung
Eintrittsgeschwindigkeit
Druckzahl und Durchflußzahl
isentroper Wirkungsgrad

Zusätzlich werden aus dem Eingabefile die Axialspalte über die axialen Schaufelkoordinaten an Nabe und Gehäuse eingelesen. Eventuelles Auf- oder Zudrehen der Schaufeln bleibt bei den Axialspalten unberücksichtigt.

STAB arbeitet zuerst jeden Betriebspunkt für sich ab, bevor es die Ergebnisse der einzelnen Punkte untereinander vergleicht. Einige Größen müssen nach dem Einlesen erst in eine für das Programm brauchbare Form umgeschrieben werden. Winkel werden ins Bogenmaß umgerechnet und mit positivem Vorzeichen versehen (Das negative Vorzeichen ist bei Dynatech Kennzeichen der Strömungswinkel am Laufrad, nicht jedoch der Schaufelwinkel des Laufrades.). Der Druck wird in Pascal umgerechnet; φ und ψ werden auf den Radius der mittleren Stromlinie bezogen.

Die eigentliche Auswertung kommt auf wenigen Programmseiten unter und soll vom programmtechnischen Aspekt nur kurz angerissen werden.

Die äquivalente Diffusionszahl Liebleins wird Stromlinie für Stromlinie und Gitter für Gitter berechnet.

Stufenweise und ohne Beachtung des Vorleitrades wird bei den Kriterien von Traupel und Koch vorgegangen.

Für Traupels Vorschrift werden zu den separaten φ und ψ noch die jeweiligen integralen Werte durch Massenstrommittlung bestimmt. Dazu wird der Massenstrom zwischen zwei benachbarten Stromröhren ermittelt und mit dem Mittelwert der zugehörigen φ bzw. ψ multipliziert. Danach wird über alle betrachteten Stromröhren aufsummiert (wandnahe Schichten gehen nicht ein) und durch den eingeschlossenen Massenstrom dividiert. Bemerkt sei, daß die integralen Ergebnisse programmintern nicht weiter verwendet werden, was mit der von Traupel abweichenden Interpretation der Kennlinien durch den Autor zusammenhängt (s. Abschnitt 5.2.).

Als nächstes werden zulässiger und tatsächlicher Enthalpiekoeffizient nach Koch errechnet. Der zulässige Wert ergibt sich aus der geometrischen Größe l/g2 (Gleichung (5.6) und Abbildung 5.6). Der tatsächliche Wert wird nach Gleichung (5.7) ermittelt und sogleich nach Lage der Geschwindigkeitsdreiecke korrigiert. Dazu dient das Unterprogramm FE, welches die Rechenoperationen durchführt, die in Abbildung 5.11 aufgezeigt sind. Hiernach wird der tatsächliche Enthalpiekoeffizient beginnend mit der Reynoldszahl korrigiert. So, wie es Koch vorschlägt, erfolgt dann die Radialspiel- und Axialspaltkorrektur.

Der Vergleich der Betriebspunkte ist mit drei Interpolationsprogrammen gekoppelt, die alle davon ausgehen, daß mindestens drei Punkte zur Interpolation zur Verfügung stehen. Alle bilden Polynome zweiten Grades, und von der Spezifik des Kriteriums hängt ab, welches der drei Unterprogramme zum Einsatz kommt.

Beim Traupelkriterium wird als erstes IP2MAX aufgerufen. Es untersucht, ob eine separate Kennlinie einen Betriebspunkt hat, der ein maximales ψ aufweist und dennoch nicht am Rande des Wertebereiches liegt. Durch diesen Punkt und seine Nachbarpunkte wird dann die Polynomfunktion gelegt und das lokale Maximum mit zugehörigem Abszissenwert gesucht. Dieser wird als PHIMIN übergeben. Seine Position innerhalb der φ der gerechneten Betriebspunkte ermöglicht mit dem Unterprogramm IP2, den Massenstrom innerhalb der gerechneten Punkte zu ermitteln, bei dem PHIMIN auftritt. Dieser Massenstrom wird als MT solange weitergeführt, bis sich bei Betrachtung weiterer Stufen ein noch größerer Wert ergibt. MT = 0 bedeutet, daß bis dato kein lokales Maximum aufgetreten ist.

Folgende Schwierigkeit kann auftreten und zu Extrapolationen führen. Bei zu kleinen Massenströmen wird φ, nachdem es kleiner wurde, plötzlich wieder größer. Das Interpolationsprogramm sucht dadurch unter ungünstigen Bedingungen seine Werte in der falschen Richtung. Sollten Extrapolationen angezeigt werden, so ist es ratsam, die Kennlinienverläufe über die eingangs erwähnten Plotdateien zu verfolgen. Gegebenenfalls ist der Massenstrom zu vergrößern. Weiterhin kann es sein, daß die zum Schluß angezeigte kritische Stufe numerisch gesehen nur minimal höher belastet ist als eine andere. Somit sollte die Stufe nicht als absolut gefährlichste und der ermittelte Massenstrom, besonders bei flachen Kennlinien, nicht als der exakt die Stabilität begrenzende angesehen werden.

Beim Kochkriterium kommt das Interpolationsprogramm IP2CH1 zum Einsatz, das im vorgegebenen Massenstrombereich den größten Wert sucht, bei dem der Enthalpiekoeffizient gerade noch kleiner ist als sein zulässiger Vergleichswert. Wird MK = 0 ausgegeben, so bedeutet das, daß nirgends das Kriterium übertreten wurde. Liegt MK etwas über dem größten vorgegebenen Massenstrom, so befinden sich alle Punkte im instabilen Bereich, und eine Extrapolation wird am Bildschirm angezeigt.

Das Maximum des isentropen Wirkungsgrades wird mit IP2MAX bestimmt.

Die Massenstrombewertung nach Lieblein erfolgt ohne Interpolation und gibt deswegen nur an, bis zu welchem gerechneten Massenstrom Instabilität herrscht. Es kann einzig empfohlen werden, die Abstände zwischen den Massenströmen klein zu halten, um ein genaues Ergebnis zu erzielen.

Für jeden errechneten kritischen Massenstrom wird über IP2 das zugehörige Ruhedruckverhältnis ermittelt. Ruhedruckverhältnis und isentroper Wirkungsgrad gelten nur für die gesamte Beschaufelung, nicht jedoch für die gesamte Maschine mit Einlaufgehäuse und nachgeschaltetem Diffusor. Andere Werte werden in der Dynatech Ergebnisdatei leider nicht abgespeichert und sind deshalb nicht greifbar.

Nochmals sei erwähnt, daß alle Extrapolationen nur am Bildschirm angezeigt werden. Steht zur Auswertung nur noch die STAB Ergebnisdatei zur Verfügung, so ist es unerläßlich zu prüfen, ob die kritischen Punkte tatsächlich innerhalb der vorgegebenen Betriebspunkte liegen. In anderen Fällen sind die Daten nicht brauchbar, und die Vorgaben müssen abgeändert werden, wozu freilich neue Dynatech Rechnungen nötig sind.

Mit dem Programmende von STAB werden sämtliche Dateien geschlossen, und die Prozedur PROC.STAB ist beendet.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Vergleich gerechneter und gemessener Daten für ausgewählte vielstufige Axialverdichter

Zur Bewertung der Stabilitätskriterien wurden für drei mehrstufige Verdichter Dynatech Rechnungen durchgeführt und Kennlinien ermittelt. Die Rechenergebnisse wurden mit dem Programm STAB ausgewertet, das nach allen zuvor beschriebenen Modellen die Stabilitätsgrenze bestimmt. Die Kurvenverläufe sind in Abbildung 8.1, Abbildung 8.2, Abbildung 8.3 aufgetragen. Die Abbildungen beinhalten auch die experimentellen Vergleichskurven zu den gerechneten Kennlinien. Im Versuch ermittelte Pumpgrenzpunkte sind besonders hervorgehoben.

Für jeden Verdichter läßt sich anhand der zugehörigen Tabelle die Ebene ersehen, die nach STAB als kritisch angesehen werden muß.

Im Anhang befinden sich noch Iso-Plotts für die Diffusionszahl D. Sie wurden für Betriebspunkte angefertigt, die in Abbildung 8.1, Abbildung 8.2, Abbildung 8.3 wiederzufinden sind. Der Buchstabe L kennzeichnet im Schriftfeld einen Pumpgrenzpunkt nach dem Liebleinkriterium, W einen Punkt nach dem Wirkungsgradkriterium. Die nachfolgende Zahl gibt die relative Drehzahl n* in Prozent wieder. Die horizontalen Linien stellen die gerechneten Stromlinien dar; die vertikalen Linien grenzen die einzelnen Leit- und Laufräder ab.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Versuchsverdichter VV94

Der Verdichter VV94 ist von allen drei untersuchten Verdichtern am besten zur Auswertung geeignet. Die Pumpgrenze ist bis hoch zur Nenndrehzahl vermessen. Die Dynatech Rechnungen sind recht genau, was sich aus der kleinen Stufenzahl und den großen Abmessungen des Verdichters ergibt. Hierdurch ist der Einfluß der Seitenwandgrenzschichten nur schwach.

Die gerechneten Kennlinien sagen immer einen größeren erreichbaren Druckanstieg voraus, als tatsächlich verwirklicht werden kann. Je steiler die Kennlinie ist, desto mehr fällt das auf. Bei Nenndrehzahl liegen alle Kriterien sehr dicht und sehr gut, was den Massenstrom anbelangt. Für die Sicherheit eines Kriteriums ist aber das Verdichterdruckverhältnis der entscheidende Parameter, da dieses als Regelgröße verwendet werden kann. Danach sagen Traupel und Lieblein etwas zu hohe π* als Pumpgrenze voraus. Das Koch- u. das Wirkungsgradkriterium liegen knapp unter der wirklichen Pumpgrenze, wobei das Kochkriterium am konservativsten ist.

Bei kleineren Drehzahlen gehen die Pumpgrenzpunkte wegen der Flachheit der Kennlinien immer weiter auseinander. Die Kriterien nach Koch und Traupel lokalisieren die Pumpgrenze immer auf der instabilen Seite, wobei letzteres für n* < 0,81 so weit im instabilen Gebiet liegt, daß es auf den gerechneten Kennlinien nicht erfaßt wird. Das Liebleinkriterium bewegt sich vom leicht instabilen Bereich bei n* = 0,9 auf die sichere Seite der Kennlinien bei n* = 0,81 bis n* = 0,6. Das Wirkungsgradmaximum liegt überall unterhalb der gemessenen Stabilitätsgrenze.

Die Iso-Plotts bei Nenndrehzahl (Abbildung 11.1, Abbildung 11.2) zeigen, daß für das Wirkungsgradkriterium nur der Nabenbereich des letzten Leitrades zu stark belastet ist. Der Punkt, den das Liebleinkriterium vorhersagt, weist bereits Überlastungen im Gehäusebereich des vorletzten Laufrades sowie im Nabenbereich der beiden letzten Leiträder auf. Diese Ergebnisse bestätigen den richtigen Bezug zwischen gerechneten und gemessenen Daten. Die Plotts bei reduzierten Drehzahlen (Abbildung 11.3, Abbildung 11.4) zeigen deutlich, wie die gefährlichen Zonen innerhalb des Verdichters nach vorn wandern. Diese richtige Tendenz gibt auch die Tabelle 8.1 wieder, denn nach STAB sind bei Nenndrehzahl entweder die letzte oder die vorletzte Stufe kritisch, und bei kleinerer Drehzahl liegen die gefährlichen Ebenen am Eintritt.

Nach der Abbildung 8.1 ist das Wirkungsgradkriterium am besten geeignet, um die Stabilitätsgrenze zu bestimmen. Die Kurve verläuft gleichmäßig und nur bis zu drei Prozentpunkten unterhalb der tatsächlichen Grenze.

relative Drehzahl

Koch Kriterium

Lieblein Kriterium

Traupel Kriterium

n* = 1,0

3. Stufe

Leitrad 4

4. Stufe

n* = 0,9

3. Stufe

Laufrad 3

4. Stufe

n* = 0,81

3. Stufe

Laufrad 3

4. Stufe

n* = 0,7

1. Stufe

Laufrad 1

(m zu groß)

n* = 0,6

1. Stufe

Laufrad 1

(m zu groß)

Tabelle 8.1: Kritische Ebenen für den 4-stufigen Versuchsverdichter VV94

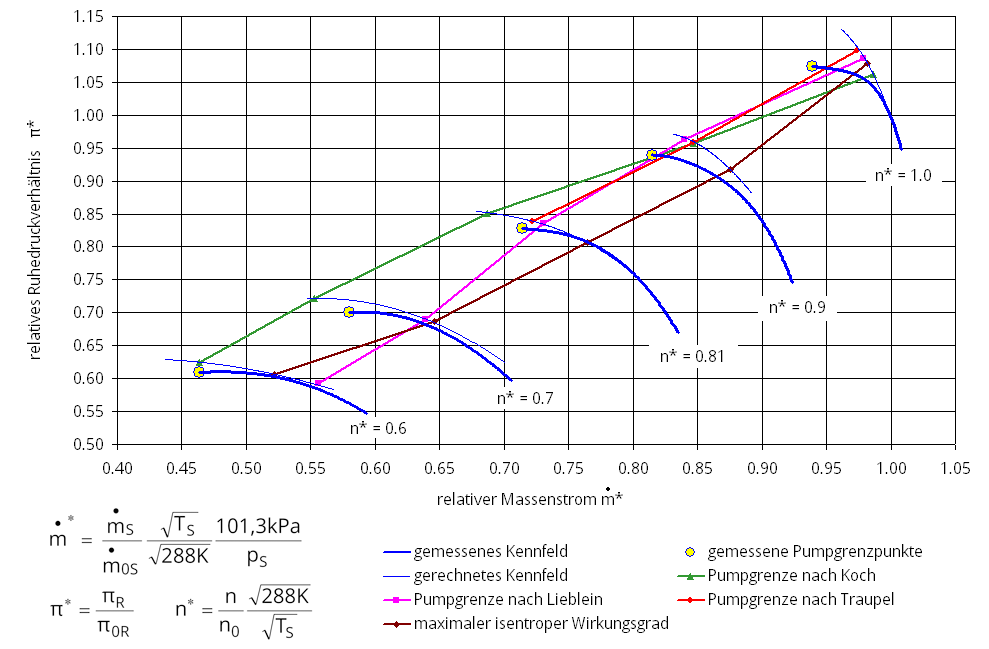
Abbildung 8.1: 4-stufiger Verdichter Vv94 mit 3,5° aufgedrehtem Vorleitrad

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Verdichter Vx4.2

Bei dem 17-stufigen Verdichter Vx4.2 wurde die Pumpgrenze nur dreimal bei niedrigen Drehzahlen angefahren. Zur Bewertung der Kriterien bei Nenndrehzahl kann in Anlehnung an das Wirkungsgradkriterium davon ausgegangen werden, daß dort die Pumpgrenze beim ca. 1,2 bis 1,3-fachen vom Auslegungsdruckverhältnis liegt. Die berechneten Modelle sagen im gesamten Bereich zu optimistische Druckanstiege voraus, wobei sie untereinander stark streuen (Abbildung 8.2). Nur das Wirkungsgradkriterium hat einen gleichmäßigen Verlauf und liegt relativ dicht an der Pumpgrenze. Die Auswertung nach Traupel und Lieblein kann nicht im gesamten Drehzahlbereich erfolgen. Bei kleinen Drehzahlen ist nach Lieblein überhaupt kein Betrieb mehr möglich. Bei Nenndrehzahl erwartet Traupel viel zu kleine Massenströme. Erst dort weisen seine Stufenkennlinien lokale Maxima auf.

Es stellt sich die Frage, ob das Kennfeldprogramm nicht viel zu gute Strömungsbedingungen errechnet und dadurch die meisten Pumpgrenzpunkte so weit im instabilen Gebiet liegen. Aus dem Iso-Plott für das Wirkungsgradmaximum bei Nenndrehzahl (Abbildung 11.5) ergibt sich, daß der Nabenbereich der beiden letzten Leiträder schwach gefährdet ist.

Tabelle 8.2 macht die Verlagerung der kritischen Ebenen mit Drehzahlreduzierung nochmals anschaulich. Die Modelle nach Traupel und Koch liefern bei Nenndrehzahl ungenügende Ergebnisse. Beide gehen vom statischen Enthalpieanstieg aus und finden entweder keinen kritischen Punkt bzw. erst dann einen Wert, wenn praktisch nicht zu erreichende Druckverhältnisse erzielt werden sollen.

relative Drehzahl

Koch Kriterium

Lieblein Kriterium

Traupel Kriterium

n* = 1,0

5. Stufe

Leitrad 16

(m zu groß)

n* = 0,95

1. Stufe

Laufrad 1

5. Stufe

n* = 0,9

1. Stufe

(m zu klein)

4. Stufe

n* = 0,85

1. Stufe

(m zu klein)

3. Stufe

Tabelle 8.2: Kritische Ebenen für den 17-stufigen Verdichter Vx4.2

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Verdichter Vx4.3

Die Ergebnisse unterscheiden sich etwas von denen des Verdichters Vx4.2. Das Wirkungsgradkriterium liegt ab n* ≥ 0,9 im stabilen Bereich. Für n* ≥ 0,95 liefern die errechneten Punkte nach Lieblein und Koch noch Resultate dicht an der Pumpgrenze. Bei kleinerer Drehzahl lassen sich nach ihnen keine Betriebspunkte mehr ermitteln (Abbildung 8.3). Tabelle 8.3 verdeutlicht wieder, wie sich die Instabilitäten bei Drehzahlverringerung zum Verdichtereintritt hin verlagern. Die Iso-Plotts in Abbildung 11.6, Abbildung 11.7, Abbildung 11.8 zeigen für alle drei ausgewählten Betriebspunkte überkritische Diffusionszahlen an.

relative Drehzahl

Koch Kriterium

Lieblein Kriterium

Traupel Kriterium

n* = 1,0

17. Stufe

Leitrad 17

13. Stufe

n* = 0,95

1. Stufe

Leitrad 12

11. Stufe

n* = 0,9

1. Stufe

(m zu klein)

5. Stufe

n* = 0,85

(m zu klein)

4. Stufe

n* = 0,8

(m zu klein)

4. Stufe

Tabelle 8.3: Kritische Ebenen für den 17-stufigen Verdichter Vx4.3

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Zusammenfassung und Ausblick

Der Vergleich zwischen gerechneten und gemessenen Daten zeigt, daß von allen untersuchten Modellen das Wirkungsgradkriterium (Betriebspunkt beim maximalen isentropen Wirkungsgrad) am besten geeignet ist, um den Arbeitsbereich eines vielstufigen Verdichters zu kleinen Massenströmen theoretisch abgrenzen zu können. Dieses Resultat ergibt sich unter der Voraussetzung, daß die Strömungsverhältnisse durch das Kennfeldrechenprogramm richtig dargestellt werden. Das ist bei hoher Stufenzahl und besonders bei kleinen Drehzahlen nicht der Fall, was für diese Maschinen eine Bewertung der Stabilitätskriterien zum jetzigen Zeitpunkt nicht zuläßt. Grundlegendes Problem ist die noch fehlerhafte Verlustbestimmung in der Dynatech Rechnung.

Erst dann, wenn das Kennfeldprogramm einer guten Genauigkeit genügt, läßt sich mit Sicherheit sagen, ob ein anderes Modell noch von Nutzen sein kann und in bestimmten Bereichen möglicherweise sogar besser liegt als das Wirkungsgradkriterium.

Zur Auswertungsprozedur werden folgende weitergehende Untersuchungen vorgeschlagen. Momentan werden wegen fehlender Vorgaben nur beschaufelungsbezogene Druckverhältnisse und Wirkungsgrade analysiert. Die Abweichungen zu maschinenbezogenen Daten sind zu bewerten und gegebenenfalls zu berücksichtigen. Die Auswertung nach dem Liebleinkriterium kann exakter gestaltet werden. Dazu muß sie mit einer Integrationsfunktion gekoppelt werden, wodurch sich die prozentual überlastete Schaufelhöhe besser bestimmen läßt, als es momentan durch die diskrete Betrachtung von Werten auf den einzelnen Stromlinien der Fall ist.

Für das Kochkriterium sind genaue Radialspaltvorgaben zu treffen.

Das Traupelkriterium sollte an Verdichtern untersucht werden, die nach dem Potentialwirbelgesetz ausgelegt sind. Für die bisher untersuchten Maschinen könnte eine größere Stromlinienanzahl von Vorteil für das Modell sein, denn dadurch käme der Wandeinfluß mehr zum tragen, und die viel zu optimistischen Werte könnten reeller werden. Problematisch ist dabei, daß für mehr als neun Stromlinien in der Dynatech Ergebnisdatei kein Speicherplatz vorgesehen ist. Alle Felder sind bis zehn dimensioniert, wobei der letzte Wert immer ein Integralausdruck über die Stromlinien ist. Die gleiche Dimensionierung gilt auch für STAB.

Abschließend möchte sich der Autor für die tatkräftige Unterstützung durch seine Betreuer Herrn Prof. Lindner von der TU Dresden und Herrn Dr. Janssen von Siemens KWU bedanken. Der Dank gilt gleichfalls allen anderen Kollegen der Gasturbinenabteilung TGRM. Sie alle haben mitgeholfen, daß die Diplomarbeit einen wirklich interessanten Einblick in dieses so wichtige Gebiet der Strömungsmechanik gebracht hat.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Literatur und Quellennachweis

[1]

Dynatech R/D Company, 17 Tudor Street, Cambridge, Massachusetts 02139, USA: HTO300 A Computer Program for the Design and Analysis of Axial Turbomachinery, Parts I, II, 1970

[2]

L. H. Smith Jr.: The Radial-Equilibrium Equation of Turbomachinery, ASME Journal of Engineering for Power (Paper No 65-WA/GTP-1), January, 1966

[3]

Lieblein/ Schwenk/ Broderick: Diffusion Factor for Estimating Losses and Limiting Blade Loadings in Axial-Flow-Compressor Blade Elements, NACA RM E53D01, 1953

[4]

O. Conrad: Belastungskriterien von Verzögerungsgittern, MTZ 26/8,1965

[5]

Johnson/ Bullock et al: Aerodynamic Design of Axial-Flow Compressors, NASA SP36,1965

[6]

Jansen/ Moffatt: The Off-Design Analysis of Axial-Flow Compressors, ASME 66-WA/GT-1, 1966

[7]

Herrig/ Emery/ Erwin: Systematic Two-Dimensional Cascade Tests of NACA65-Series Compressor Blades at Low Speeds, NACA TN 3916, 1957 (Supersedes TN 3916, RM L51G31)

[8]

Emery/ Dunavant: Two-Dimensional Cascade Tests of NACA65-(C10A10)10 Blade Sections at Typical Compressor Hub Conditions for Speeds up to Choking, NACA RM L57H05, 1957

[9]

W. Jansen: The Application of End-Wall Boundary-Layer-Effects in the Performance Analysis of Axial Compressors, ASME 67-WA/GT-11, 1967

[10]

F. E. Mc Caughan: Bifurcation Analysis of Axial Flow Compressor Stability, SIAM J. APPL. MATH. Vol. 50, No 5, 1990

[11]

E. M. Greitzer: Surge and Rotating Stall in Axial Flow Compressors, Parts I, II, ASME Journal of Engineering for Power, 1967

[12]

E. Lindner: Taschenbuch Maschinenbau, Bd. 5, Turboverdichter, Berlin, 1989

[13]

W. Traupel: Thermische Turbomaschinen, 2. Bd., Geänderte Betriebsbedingungen, Regelung, Mechanische Probleme, Temperaturprobleme, Springer Verlag Berlin und Heidelberg, 1982

[14]

S. Lieblein: Loss and Stall Analysis of Compressor Cascades, Transaction of the ASME, Journal of Basic Engineering (Paper No 58-A-91), 1959

[15]

C. C. Koch: Stalling Pressure Rise Capability of Axial Flow Compressor Stages, ASME Journal of Engineering for Power 103(4), 645-656 (Oct 01, 1981), 81-GT-3

[16]

E. Lindner: Vorlesung Turboverdichter, TU Dresden, Institut für Strömungsmechanik, 1991

[17]

M. V. Casey: A Mean Line Prediction Method for Estimating the Performance Characteristic of an Axial Compressor Stage, Mechanical Engineering Publications Ltd., London, 1987

[18]

D. Traulsen: Axialverdichterprüfstand zur Untersuchung von Randzonenströmungen, Fortschrittberichte, VDI Reihe 7 No 161, Düsseldorf, 1989

[19]

W. Albring: Angewandte Strömungslehre, 6. Auflage, Berlin, 1990

[20]

Sovran/ Klomp: Experimentally Determined Optimum Geometries for Rectilinear Diffusers with Rectangular, Conical or Annular Cross Section, Fluid Mechanics of Internal Flow, Elsevier Publishing, Amsterdam, Netherlands, 1967

[21]

A. I. Mechanikov et al: Untersuchung von Verdichtercharakteristiken stationärer Gasturbinenanlagen, Teploenergetika No 3, 1983 (russisch)

[22]

A. O. Burmaskov et al: Versuche zur Verdichterstabilität während der Inbetriebnahme der PGU200 Gas- und Dampfturbinen Anlage, Energomasinostroenie No 11, 1975 (russisch)

[23]

Suter/ Späti: Die Abreißgrenze mehrstufiger Axialverdichter, Turboforum No 2, 1972

Abbildung 5.5 Bild links, Abbildung 5.6 und Abbildung 5.11 aus [15] © ASME mit freundlicher Genehmigung. Alle anderen Abbildungen vom Autor Axel Ebert.

Inhaltsverzeichnis | Formelzeichen | Literatur | ▲ Seitenanfang

Übersicht

Fluid Technology

Net Technology

Dropdown menue with CSS

Airalo eSIM

Designer

Axel Ebert

Strömungsmechanik

Pumpgrenze Verdichter